19.(本小题共12分)
设数列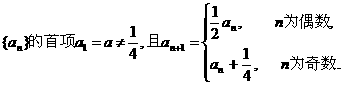
记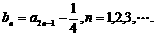
(Ⅰ)求a2,a3;
(Ⅱ)判断数列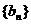 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)求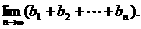
[答案]
[详解]
解:(I)
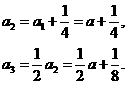
(II)
因为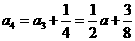 ,所以
,所以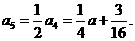
所以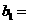
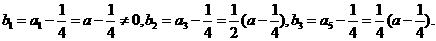
猜想: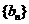 是公比为
是公比为 的等比数列.
的等比数列.
证明如下:
因为
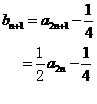
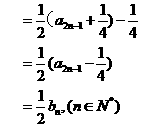
所以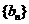 是首项为
是首项为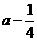 ,公比为
,公比为 的等比数列.
的等比数列.
(III)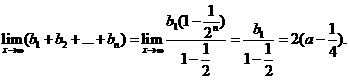
[名师指津]
数列类型题,数列通项公式的递推公式经常在已知条件中给出,利用列举、叠加、叠乘等方法求之
通项公式的方法应掌握,另外递推公式与数学归纳法思想一致,数学归纳法证明方法经常在此类
题中运用.等差等比数列的通项公式及前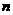 项和公式的求法和运用,等差等比数列的性质做为本
项和公式的求法和运用,等差等比数列的性质做为本
章复习的重点内容.
- 答案

