9.把一同排6张座位编号为1,2,3,4,5,6的电影票全部分给4个人,每人至少分1张,至多分2张,且这两张票具有连续的编号,那么不同的分法种数是 ( )
A.168 B.96 C.72 D.144
解:本题主要关键是抓连续编号的2张电影票的情况,可分四种情况:
情况一:连续的编号的电影票为1,2;3,4;5,6,这时分法种数为
情况二:连续的编号的电影票为1,2;4,5,这时分法种数为
情况三:连续的编号的电影票为2,3;4,5;这时分法种数为
情况四:连续的编号的电影票为2,3;5,6,这时分法种数为
综上, 把一同排6张座位编号为1,2,3,4,5,6的电影票全部分给4个人,每人至少分1张,至多分2张,且这两张票具有连续的编号,那么不同的分法种数是 +3
+3 =144(种)
=144(种)
8.已知a、b、c是直线,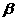 是平面,给出下列命题:
是平面,给出下列命题:
①若 ;
;
②若 ;
;
③若 ;
;
④若a与b异面,且 相交;
相交;
⑤若a与b异面,则至多有一条直线与a,b都垂直.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
解:①③④⑤是假命题,②是真命题,选(A)
7.在 这四个函数中,当
这四个函数中,当 时,使
时,使 恒成立的函数的个数是 ( )
恒成立的函数的个数是 ( )
A.0 B.1 C.2 D.3
解:∵当 时,
时, ,即当
,即当 时,使log2x,
时,使log2x,
 恒成立,其它3个函数都可以举出反例当
恒成立,其它3个函数都可以举出反例当 时,使
时,使 不成立(这里略),选(B)
不成立(这里略),选(B)
6.双曲线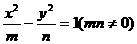 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线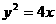 的焦点重合,则mn的值为 ( )
的焦点重合,则mn的值为 ( )
A.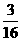 B.
B.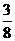 C.
C.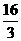 D.
D.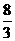
解:抛物线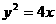 的焦点为(1,0),∴
的焦点为(1,0),∴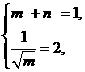 得m=
得m=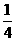 ,n=
,n= ,∴mn=
,∴mn=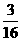 ,选(A)
,选(A)
5.木星的体积约是地球体积的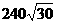 倍,则它的表面积约是地球表面积的 ( )
倍,则它的表面积约是地球表面积的 ( )
A.60倍 B.60 倍 C.120倍 D.120
倍 C.120倍 D.120 倍
倍
解:设木星的半径为r1,地球的半径为r2由题意得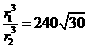 ,则木星的表面积∶地球的表面积=
,则木星的表面积∶地球的表面积= ,选(C)
,选(C)
3.已知向量a=(-2,2),b=(5,k).若|a+b|不超过5,则k的取值范围是 ( )
A.[-4,6] B.[-6,4] C.[-6,2] D.[-2,6]
解:∵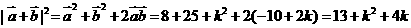 ,由题意得k2+4k+-12≤0,解得-6≤k≤2,即k的取值范围为[-6,2],选(C)
,由题意得k2+4k+-12≤0,解得-6≤k≤2,即k的取值范围为[-6,2],选(C)
2.对任意实数a,b,c,给出下列命题:
①“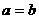 ”是“
”是“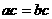 ”充要条件; ②“
”充要条件; ②“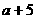 是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
解:①是假命题,∵由ac=bc推不出a=b;②是真命题;③是假命题;④是真命题,∵“a<3”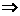 “a<5”,选(B)
“a<5”,选(B)
1.设P、Q为两个非空实数集合,定义集合P+Q=
 ,则P+Q中元素的个数是 ( )
,则P+Q中元素的个数是 ( )
A.9 B.8 C.7 D.6
解:集合P中和集合Q中各选一个元素可组成的组合数为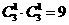 其对应的和有一个重复:0+6=1+5,
其对应的和有一个重复:0+6=1+5,
故P+Q中的元素有8个,选(B)
22.(本小题满分14分)
已知不等式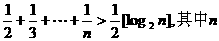 为大于2的整数,
为大于2的整数,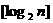 表示不超过
表示不超过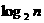 的最大整数. 设数列
的最大整数. 设数列 的各项为正,且满足
的各项为正,且满足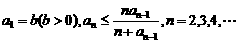
(Ⅰ)证明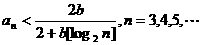
(Ⅱ)猜测数列 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当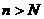 时,对任意b>0,都有
时,对任意b>0,都有
2005年普通高等学校招生全国统一考试(湖北卷)

 的图象大致是 ( )
的图象大致是 ( )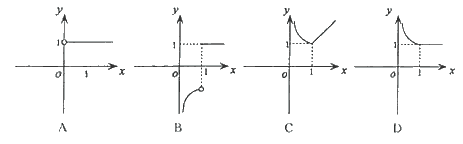
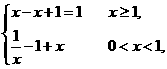 选(D)
选(D)