21.(本小题满分12分)
设A、B是椭圆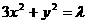 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定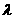 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的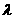 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
20.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,
,
BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.

19.(本小题满分12分)
某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机
会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。
如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在
一年内李明参加驾照考试次数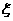 的分布列和
的分布列和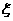 的期望,并求李明在一年内领到驾照的概率.
的期望,并求李明在一年内领到驾照的概率.
16.某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 元.
解:从单价上考虑, 每袋35千克的单价要低于每袋24千克的单价,故应优先考虑购买每袋35千克的包装
设每袋35千克的包装购买x袋,每袋24千克的包装购买y袋,则有
当x=4时,y=0,这时共购进化工原料140千克,需要花费140×4=560元;
当x=3时,y=1,这时共购进化工原料129千克,需要花费540元;
当x=2时,y=2,这时共购进化工原料118千克,需要花费520元;
当x=1时,y=3,这时共购进化工原料107千克,需要花费500元
综上, 在满足需要的条件下,最少要花费500元.
15.设等比数列 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
.
解:由题意可知q≠1,∴可得2(1-qn)=(1-qn+1)+(1-qn+2),即q2+q-2=0,解得q=-2或q=1(不合题意,舍去),∴q=-2.
14.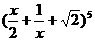 的展开式中整理后的常数项为
.
的展开式中整理后的常数项为
.
解: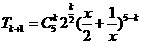 ,其中k满足0≤k≤5.k∈N,
,其中k满足0≤k≤5.k∈N,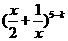 的通项公式为
的通项公式为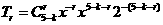 ,
,
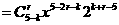 ,其中0≤r≤5-k,r∈N,令5-2r-k=0,邵k+2r=5,解得k=1,r=2;k=3,r=1;k=5,r=0
,其中0≤r≤5-k,r∈N,令5-2r-k=0,邵k+2r=5,解得k=1,r=2;k=3,r=1;k=5,r=0
当k=1,r=2时,得展开式中项为 ;当k=3,r=1时, 得展开式中项为
;当k=3,r=1时, 得展开式中项为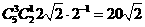 ;当k=5,r=0时得展开式中项为
;当k=5,r=0时得展开式中项为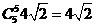 ,综上
,综上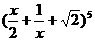 的展开式中整理后的常数项为
的展开式中整理后的常数项为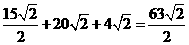
12.以平行六面体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率p为 ( )
A. B.
B.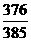 C.
C.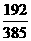 D.
D.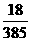
解:以平行六面体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形共有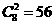 个, 从中随机取出两个三角形共有
个, 从中随机取出两个三角形共有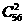 =28×55种取法,其中两个三角形共面的为
=28×55种取法,其中两个三角形共面的为 ,故不共面的两个三角形共有(28×55-12×6)种取法,∴.以平行六面体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率p为
,故不共面的两个三角形共有(28×55-12×6)种取法,∴.以平行六面体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率p为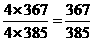 ,选(A)
,选(A)
第Ⅱ卷(非选择题 共90分)
第Ⅱ卷用0.5毫米黑色的签字或黑色墨水钢笔直接答在答题卡上。答在试题卷上无效。

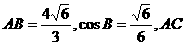 边上的中线BD=
边上的中线BD=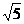 ,求sinA的值.
,求sinA的值.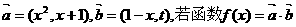 在区间(-1,1)上是增函数,
在区间(-1,1)上是增函数, 不超过5,则k的取值范围是
.
不超过5,则k的取值范围是
. ,由题意得k2+4k+-12≤0,解得-6≤k≤2,即k的取值范围为[-6,2]
,由题意得k2+4k+-12≤0,解得-6≤k≤2,即k的取值范围为[-6,2]