2025年同步练习册人民教育出版社高中化学选择性必修第一册人教版A山东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年同步练习册人民教育出版社高中化学选择性必修第一册人教版A山东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. 黑火药是我国古代的四大发明之一,其爆炸的热化学方程式为
$S(s) + 2KNO_{3}(s) + 3C(s) = K_{2}S(s) + N_{2}(g) + 3CO_{2}(g)\ \ \Delta H = x\ kJ· mol^{-1}$
已知:碳的燃烧热$\Delta H_{1} = a\ kJ· mol^{-1}$
$S(s) + 2K(s) = K_{2}S(s)\ \ \Delta H_{2} = b\ kJ· mol^{-1}$
$2K(s) + N_{2}(g) + 3O_{2}(g) = 2KNO_{3}(s)\ \ \Delta H_{3} = c\ kJ· mol^{-1}$
则$x$为(
A.$3a + b - c$
B.$c - 3a - b$
C.$a + b - c$
D.$c - a - b$
$S(s) + 2KNO_{3}(s) + 3C(s) = K_{2}S(s) + N_{2}(g) + 3CO_{2}(g)\ \ \Delta H = x\ kJ· mol^{-1}$
已知:碳的燃烧热$\Delta H_{1} = a\ kJ· mol^{-1}$
$S(s) + 2K(s) = K_{2}S(s)\ \ \Delta H_{2} = b\ kJ· mol^{-1}$
$2K(s) + N_{2}(g) + 3O_{2}(g) = 2KNO_{3}(s)\ \ \Delta H_{3} = c\ kJ· mol^{-1}$
则$x$为(
A
)。A.$3a + b - c$
B.$c - 3a - b$
C.$a + b - c$
D.$c - a - b$
答案:
15. A 解析 由碳的燃烧热,可得热化学方程式①:$\mathrm{C(s)+O_2(g)=CO_2(g)}$ $\Delta H_1=a\ \mathrm{kJ· mol^{-1}}$。对题目中涉及的其他热化学方程式依次编号:②、③、④,根据盖斯定律,②=①$× 3+$③—④得$\Delta H=\Delta H_1×3+\Delta H_3-\Delta H_4$,即$x=3a+b-c$,故A 项正确。
16. (12 分)根据下列叙述写出相应的热化学方程式。
(1)已知$16\ g$硫粉完全燃烧时放出$148.4\ kJ$的热量,写出表示硫粉燃烧热的热化学方程式。
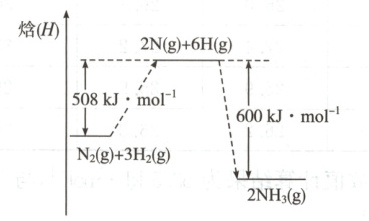
(2)在$25^{\circ}C$和$101\ kPa$时,$N_{2}$与$H_{2}$反应过程中物质的焓变如图。写出该反应的热化学方程式。
(3)在$25^{\circ}C$和$101\ kPa$时,$8\ g\ CH_{4}$完全燃烧生成液态水时放出$445.15\ kJ$的热量。写出$CH_{4}$燃烧的热化学方程式。
(1)已知$16\ g$硫粉完全燃烧时放出$148.4\ kJ$的热量,写出表示硫粉燃烧热的热化学方程式。
(2)在$25^{\circ}C$和$101\ kPa$时,$N_{2}$与$H_{2}$反应过程中物质的焓变如图。写出该反应的热化学方程式。

(3)在$25^{\circ}C$和$101\ kPa$时,$8\ g\ CH_{4}$完全燃烧生成液态水时放出$445.15\ kJ$的热量。写出$CH_{4}$燃烧的热化学方程式。
答案:
16.答案
(1)$\mathrm{S(s)+O_2(g)=SO_2(g)}$ $\Delta H=-296.8\ \mathrm{kJ· mol^{-1}}$
(2)$\mathrm{N_2(g)+3H_2(g)\rightleftharpoons 2NH_3(g)}$ $\Delta H=-92\ \mathrm{kJ· mol^{-1}}$
(3)$\mathrm{CH_4(g)+2O_2(g)=CO_2(g)+2H_2O(l)}$ $\Delta H=-890.3\ \mathrm{kJ· mol^{-1}}$
解析
(1)16 g 硫粉的物质的量为 0.5 mol,完全燃烧时放出 148.4 kJ 的热量,则 1 mol 硫粉完全燃烧放出 296.8 kJ 的热量,据此可写出表示硫粉燃烧热的热化学方程式。
(2)由题图可以看出反应物和生成物的能量差值为 $600\ \mathrm{kJ}-508\ \mathrm{kJ}=92\ \mathrm{kJ}$,该反应的热化学方程式为 $\mathrm{N_2(g)+3H_2(g)\rightleftharpoons 2NH_3(g)}$ $\Delta H=-92\ \mathrm{kJ· mol^{-1}}$。
(3)根据题意,1 mol $\mathrm{CH_4}$ 完全燃烧生成液态水放出热量为 $445.15\ \mathrm{kJ}×\frac{16\ \mathrm{g}}{8\ \mathrm{g}}=890.3\ \mathrm{kJ}$,$\mathrm{CH_4}$ 燃烧的热化学方程式为 $\mathrm{CH_4(g)+2O_2(g)=CO_2(g)+2H_2O(l)}$ $\Delta H=-890.3\ \mathrm{kJ· mol^{-1}}$。
(1)$\mathrm{S(s)+O_2(g)=SO_2(g)}$ $\Delta H=-296.8\ \mathrm{kJ· mol^{-1}}$
(2)$\mathrm{N_2(g)+3H_2(g)\rightleftharpoons 2NH_3(g)}$ $\Delta H=-92\ \mathrm{kJ· mol^{-1}}$
(3)$\mathrm{CH_4(g)+2O_2(g)=CO_2(g)+2H_2O(l)}$ $\Delta H=-890.3\ \mathrm{kJ· mol^{-1}}$
解析
(1)16 g 硫粉的物质的量为 0.5 mol,完全燃烧时放出 148.4 kJ 的热量,则 1 mol 硫粉完全燃烧放出 296.8 kJ 的热量,据此可写出表示硫粉燃烧热的热化学方程式。
(2)由题图可以看出反应物和生成物的能量差值为 $600\ \mathrm{kJ}-508\ \mathrm{kJ}=92\ \mathrm{kJ}$,该反应的热化学方程式为 $\mathrm{N_2(g)+3H_2(g)\rightleftharpoons 2NH_3(g)}$ $\Delta H=-92\ \mathrm{kJ· mol^{-1}}$。
(3)根据题意,1 mol $\mathrm{CH_4}$ 完全燃烧生成液态水放出热量为 $445.15\ \mathrm{kJ}×\frac{16\ \mathrm{g}}{8\ \mathrm{g}}=890.3\ \mathrm{kJ}$,$\mathrm{CH_4}$ 燃烧的热化学方程式为 $\mathrm{CH_4(g)+2O_2(g)=CO_2(g)+2H_2O(l)}$ $\Delta H=-890.3\ \mathrm{kJ· mol^{-1}}$。
17. (12 分)(1)能源是国民经济发展的基础,我国目前使用的能源主要是化石燃料。
已知:
①$C(s) + O_{2}(g) = CO_{2}(g)\ \ \Delta H = -393.5\ kJ· mol^{-1}$
②$2H_{2}(g) + O_{2}(g) = 2H_{2}O(g)\ \ \Delta H = -483.6\ kJ· mol^{-1}$
③$2H_{2}(g) + O_{2}(g) = 2H_{2}O(l)\ \ \Delta H = -571.6\ kJ· mol^{-1}$
④$2CO(g) + O_{2}(g) = 2CO_{2}(g)\ \ \Delta H = -566.0\ kJ· mol^{-1}$
⑤$2C_{2}H_{2}(g) + 5O_{2}(g) = 4CO_{2}(g) + 2H_{2}O(l)\ \ \Delta H = -2599.2\ kJ· mol^{-1}$
a. 计算煤的气化反应$C(s) + H_{2}O(g) = CO(g) + H_{2}(g)$的$\Delta H =$
b. 写出由$C(s)$与$H_{2}(g)$反应生成$C_{2}H_{2}(g)$的热化学方程式:
(2)已知:①$2O_{2}(g) + N_{2}(g) = N_{2}O_{4}(l)\ \ \Delta H_{1}$
②$N_{2}(g) + 2H_{2}(g) = N_{2}H_{4}(l)\ \ \Delta H_{2}$
③$O_{2}(g) + 2H_{2}(g) = 2H_{2}O(g)\ \ \Delta H_{3}$
④$2N_{2}H_{4}(l) + N_{2}O_{4}(l) = 3N_{2}(g) + 4H_{2}O(g)\ \ \Delta H_{4} = -1048.9\ kJ· mol^{-1}$
a. 用$\Delta H_{1}$、$\Delta H_{2}$、$\Delta H_{3}$的代数式表示:$\Delta H_{4} =$
b. $N_{2}H_{4}$和$N_{2}O_{4}$可作为火箭推进剂的主要原因是
已知:
①$C(s) + O_{2}(g) = CO_{2}(g)\ \ \Delta H = -393.5\ kJ· mol^{-1}$
②$2H_{2}(g) + O_{2}(g) = 2H_{2}O(g)\ \ \Delta H = -483.6\ kJ· mol^{-1}$
③$2H_{2}(g) + O_{2}(g) = 2H_{2}O(l)\ \ \Delta H = -571.6\ kJ· mol^{-1}$
④$2CO(g) + O_{2}(g) = 2CO_{2}(g)\ \ \Delta H = -566.0\ kJ· mol^{-1}$
⑤$2C_{2}H_{2}(g) + 5O_{2}(g) = 4CO_{2}(g) + 2H_{2}O(l)\ \ \Delta H = -2599.2\ kJ· mol^{-1}$
a. 计算煤的气化反应$C(s) + H_{2}O(g) = CO(g) + H_{2}(g)$的$\Delta H =$
+131.3 kJ·mol^{-1}
。b. 写出由$C(s)$与$H_{2}(g)$反应生成$C_{2}H_{2}(g)$的热化学方程式:
2C(s)+H_2(g)=C_2H_2(g) ΔH=+226.8 kJ·mol^{-1}
。(2)已知:①$2O_{2}(g) + N_{2}(g) = N_{2}O_{4}(l)\ \ \Delta H_{1}$
②$N_{2}(g) + 2H_{2}(g) = N_{2}H_{4}(l)\ \ \Delta H_{2}$
③$O_{2}(g) + 2H_{2}(g) = 2H_{2}O(g)\ \ \Delta H_{3}$
④$2N_{2}H_{4}(l) + N_{2}O_{4}(l) = 3N_{2}(g) + 4H_{2}O(g)\ \ \Delta H_{4} = -1048.9\ kJ· mol^{-1}$
a. 用$\Delta H_{1}$、$\Delta H_{2}$、$\Delta H_{3}$的代数式表示:$\Delta H_{4} =$
2ΔH_3-2ΔH_2-ΔH_1
。b. $N_{2}H_{4}$和$N_{2}O_{4}$可作为火箭推进剂的主要原因是
反应放热量大、产生大量气体
。
答案:
17.答案
(1)a.$+131.3\ \mathrm{kJ· mol^{-1}}$ b.$\mathrm{2C(s)+H_2(g)=C_2H_2(g)}$ $\Delta H=+226.8\ \mathrm{kJ· mol^{-1}}$
(2)a.$2\Delta H_3-2\Delta H_2-\Delta H_1$ b. 反应放热量大、产生大量气体
解析
(1)a. 根据盖斯定律,①—②$× \frac{1}{2}$—④$× \frac{1}{2}$得 $\mathrm{C(s)+H_2O(g)=CO(g)+H_2(g)}$, $\Delta H=-393.5\ \mathrm{kJ· mol^{-1}}-(-483.6\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}-(-566.0\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}=+131.3\ \mathrm{kJ· mol^{-1}}$。
b. 根据盖斯定律,由①$× 2+$③$× \frac{1}{2}$—⑤$× \frac{1}{2}$,得 $\mathrm{2C(s)+H_2(g)=C_2H_2(g)}$, $\Delta H=-393.5\ \mathrm{kJ· mol^{-1}}×2+(-571.6\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}-(-2599.2\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}=+226.8\ \mathrm{kJ· mol^{-1}}$。
(2)a. 根据盖斯定律,$\Delta H_4=2\Delta H_3-2\Delta H_2-\Delta H_1$。
b. $\mathrm{N_2H_4}$ 有强还原性,$\mathrm{N_2O_4}$ 有强氧化性,两者在一起发生自发的氧化还原反应,反应放热量大,产生大量气体,所以 $\mathrm{N_2H_4}$ 和 $\mathrm{N_2O_4}$ 可以作为火箭的推进剂。
(1)a.$+131.3\ \mathrm{kJ· mol^{-1}}$ b.$\mathrm{2C(s)+H_2(g)=C_2H_2(g)}$ $\Delta H=+226.8\ \mathrm{kJ· mol^{-1}}$
(2)a.$2\Delta H_3-2\Delta H_2-\Delta H_1$ b. 反应放热量大、产生大量气体
解析
(1)a. 根据盖斯定律,①—②$× \frac{1}{2}$—④$× \frac{1}{2}$得 $\mathrm{C(s)+H_2O(g)=CO(g)+H_2(g)}$, $\Delta H=-393.5\ \mathrm{kJ· mol^{-1}}-(-483.6\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}-(-566.0\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}=+131.3\ \mathrm{kJ· mol^{-1}}$。
b. 根据盖斯定律,由①$× 2+$③$× \frac{1}{2}$—⑤$× \frac{1}{2}$,得 $\mathrm{2C(s)+H_2(g)=C_2H_2(g)}$, $\Delta H=-393.5\ \mathrm{kJ· mol^{-1}}×2+(-571.6\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}-(-2599.2\ \mathrm{kJ· mol^{-1}})× \frac{1}{2}=+226.8\ \mathrm{kJ· mol^{-1}}$。
(2)a. 根据盖斯定律,$\Delta H_4=2\Delta H_3-2\Delta H_2-\Delta H_1$。
b. $\mathrm{N_2H_4}$ 有强还原性,$\mathrm{N_2O_4}$ 有强氧化性,两者在一起发生自发的氧化还原反应,反应放热量大,产生大量气体,所以 $\mathrm{N_2H_4}$ 和 $\mathrm{N_2O_4}$ 可以作为火箭的推进剂。
查看更多完整答案,请扫码查看


