《2026年学易优高考二轮总复习物理》

9. (2025·湖南长沙高三期中)如图所示,质量$M=1$ kg、长$L=1$ m的木板静止在光滑水平面上,质量为$m=2$ kg、可视为质点的物块以初速度$v_0=4$ m/s滑上木板的左端,物块与木板之间的动摩擦因数为$\mu=0.2$,在物块滑上木板的同时,给木板施加一个水平向右的恒力$F$。恒力$F$大小不同,物块在木板上相对于木板滑动的路程$s$不同,最大静摩擦力等于滑动摩擦力,重力加速度$g$取10 m/s$^2$。

(1)若$F=0$,物块滑离木板时,求滑块和木板的速度大小；
(2)若物块恰好不从左端滑离木板,求物块与木板因摩擦产生的热量；
(3)若物块恰好到达木板中点处二者速度相同,求物块与木板整个运动过程中因摩擦产生的热量。

答案： 9.答案：
(1)$\frac{10}{3}m/s$ $\frac{4}{3}m/s$
(2)$\frac{8}{3}J$
(3)$4J$
解析：
(1)根据题意，由动量守恒定律有$mv_{0}=mv_{1}+Mv_{2}$
由能量守恒定律有$\frac{1}{2}mv_{0}^{2}=\frac{1}{2}mv_{1}^{2}+\frac{1}{2}Mv_{2}^{2}+\mu mgL$
联立解得$v_{1}=\frac{10}{3}m/s$，$v_{2}=\frac{4}{3}m/s$。
(2)对物块，由牛顿第二定律有$\mu mg=ma_{0}$
解得$a_{0}=2m/s^{2}$
当物块恰不从木板左端滑出时，对整体，由牛顿第二定律有$F_{2}=(M + m)a_{0}$
解得$F_{2}=6N$
木板的加速度$F_{2}+\mu mg=Ma_{1}$，解得$a_{1}=10m/s^{2}$
相对运动过程$v = v_{0}-a_{0}t_{0}=a_{1}t_{0}$
$t_{0}=\frac{1}{3}s$，$v=\frac{10}{3}m/s$
相对滑过的路程$s=\frac{v_{0}+v}{2}t_{0}-\frac{v}{2}t_{0}=\frac{2}{3}m$
摩擦产生的热量$Q=\mu mgs=\frac{8}{3}J$。
(3)由于$\frac{L}{2}=\frac{1}{2}m ＜ s=\frac{2}{3}m$
结合上一问可知，物块将从木板的左端滑离
因此摩擦产生的热量$Q=\mu mg·\frac{L}{2}×2=4J$。

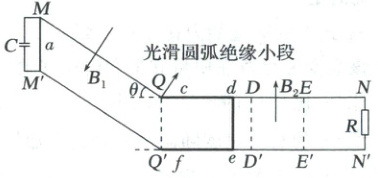
10. (2025·重庆巴蜀中学二模)如图所示,有两条不计电阻的平行光滑金属导轨$MQN$、$M'Q'N'$,导轨间距$L=0.5$ m,其中$MQ$、$M'Q'$段倾斜放置,倾斜角$\theta=37°$,$MQ=M'Q'=4$ m,$QN$、$Q'N'$段水平放置,两段之间通过一小段(大小可忽略)光滑圆弧绝缘材料平滑相连,在倾斜导轨左端连接一电容$C=2$ F的电容器,在$N$和$N'$两端与电阻$R=0.1$ $\Omega$相连,在倾斜导轨$MQ$、$M'Q'$区域内加有垂直于倾斜导轨平面向下的匀强磁场$B_1=2$ T,在水平导轨的$DD'E'E$区域内加有垂直水平导轨平面向上的匀强磁场$B_2=0.8$ T,$DD'$、$EE'$均与导轨垂直,且$DE=D'E'=L=0.5$ m,$cdef$是质量为$3m$、各边长度均为$L$的开口向左的U形金属框,已知其$de$边电阻为$R=0.1$ $\Omega$,其余各段电阻可忽略不计,开始时紧挨导轨静置于$DD'E'E$左侧外,一不计电阻的质量为$m$的金属棒$a$紧贴$MM'$从静止释放,使其向下滑行,越过$QQ'$后与U形金属框发生碰撞,碰后粘在一起形成一个正方形导体框沿导轨穿过磁场$B_2$区域。已知:$m=1$ kg,不计一切摩擦,重力加速度$g=10$ m/s$^2$。求:

(1)金属棒$a$在倾斜导轨下滑的加速度大小(提示$I=\dfrac{\Delta q}{\Delta t}=\dfrac{C\Delta U}{\Delta t}$)；
(2)$de$边刚进入磁场$B_2$区域时的速度大小；
(3)整个过程中电阻$R$上产生的焦耳热。

答案： 10.答案：
(1)$2m/s^{2}$
(2)$1m/s$
(3)$0.48J$
解析：
(1)金属棒a沿倾斜轨道向下滑行过程中有$C=\frac{\Delta Q}{\Delta U}$
又$\Delta Q=I\Delta t$，所以电流为$I=C\frac{\Delta U}{\Delta t}$
则由牛顿第二定律$mg\sin\theta - B_{1}\frac{C\Delta U}{\Delta t}L = ma$
又有$\Delta U = B_{1}L\Delta v$
则$mg\sin\theta - B_{1}\frac{CB_{1}L\Delta v}{\Delta t}=ma$
又因为$a=\frac{\Delta v}{\Delta t}$，所以可求得金属棒加速度为$a=\frac{mg\sin\theta}{m + B_{1}^{2}L^{2}C}=2m/s^{2}$。
(2)金属棒a沿倾斜轨道向下滑行过程由运动学公式得$v=\sqrt{2aL_{MQ}} = 4m/s$
金属棒a越过QQ'后与U形金属框发生碰撞，由动量守恒定律$mv=(m + 3m)v_{1}$
解得$v_{1}=1m/s$
此后一起匀速向右运动直到de边进入磁场$B_{2}$区域，即de边进入磁场$B_{2}$区域时速度为$1m/s$。
(3)在de边进入磁场区域时，de边左侧电阻为0，即右侧的电阻R被短路，无电流。此时回路总电阻就为de边的电阻R
则碰后粘在一起全部进入磁场$B_{2}$区域过程，根据动量定理有$-B_{2}\overline{I}_{2}· L·\Delta t = 4mv_{2}-4mv_{1}$
其中$\overline{I}_{2}=\frac{\overline{E}}{R}=\frac{\Delta\Phi}{R\Delta t}=\frac{B_{2}L^{2}}{\Delta tR}$
即$-B_{2}\frac{B_{2}L^{2}}{R}L = 4mv_{2}-4mv_{1}$
解得$v_{2}=0.8m/s$
在cf边进出磁场时，此时右侧de边和电阻器组成并联电路，此时总电阻为$0.5R$，则导体框一起全部穿出磁场$B_{2}$区域过程，同理有$-B_{2}\frac{B_{2}L^{2}}{0.5R}L = 4mv_{3}-4mv_{2}$
解得$v_{3}=0.4m/s$
所以此过程中电路产生的总焦耳热$Q=\frac{1}{2}·4mv_{2}^{2}-\frac{1}{2}·4mv_{3}^{2}$
电阻R上产生的焦耳热为$Q_{R}=\frac{R}{R + R}Q$
联立解得$Q_{R}=0.48J$。