《2026年学易优高考二轮总复习物理》

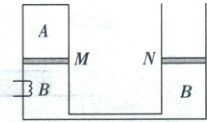
1.(2025·安徽滁州二模)如图所示,内壁光滑、高度均为$ 2h $的两个绝热汽缸底部由细管连通,左侧汽缸上端封闭,右侧汽缸上端开口与大气相通,两汽缸中面积均为$ S $的绝热活塞$ M $、$ N $密闭两部分理想气体$ A $、$ B $。开始时,气体$ A $、$ B $温度均为$ T $,活塞$ M $、
$ N $均静止在距汽缸底部$ h $处。已知活塞$ M $、$ N $的质量分别为$ 2m $和$ m $,大气压强为$ p_{0} $,重力加速度为$ g $,细管内气体体积忽略不计。
(1)求气体$ A $的压强；
(2)缓慢加热气体$ B $,使其温度升至$ \frac{4}{3}T $稳定时,
求活塞$ N $距汽缸底部的高度；
(3)上述加热过程中,若$ B $吸收的热量为$ Q $,求$ B $
的内能增加量。

答案： 1.答案：
(1)$p_{0} - \frac{mg}{S}$
(2)$\frac{5h}{3}$
(3)$Q - \frac{2}{3}(p_{0}S + mg)h$
解析：
(1)对活塞$M、N$受力分析，根据共点力平衡条件，有$p_{A}S + 2mg = p_{B}S$，$p_{0}S + mg = p_{B}S$
联立解得$p_{A} = p_{0} - \frac{mg}{S}$，$p_{B} = p_{0} + \frac{mg}{S}$。
(2)缓慢加热气体$B$，使其温度升至$\frac{4}{3}T$，在此过程中压强不变，
根据盖-吕萨克定律，有$\frac{2hS}{T} = \frac{h'S}{\frac{4}{3}T}$，得$h' = \frac{8h}{3}$
活塞$N$距汽缸底部的高度为$\Delta h = \frac{8h}{3} - h = \frac{5h}{3}$。
(3)在加热过程中，$B$中气体对外做功$W = - p_{B} · \Delta V = - (p_{0}S + mg) · \frac{2h}{3}$
根据热力学第一定律$\Delta U = W + Q$
解得$\Delta U = Q - \frac{2}{3}(p_{0}S + mg)h$。

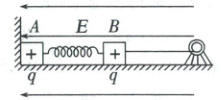
2.(2025·河南开封二模)如图所示,质量都为$ m $的物块$ A $、$ B $静止在光滑的水平面上,$ A $、$ B $之间用绝缘轻弹簧连接,$ A $紧靠墙壁,匀强电场的方向水平向左,电场强度大小为$ E $,$ A $、$ B $带电荷量均为$ q $的正电荷,$ B $通过轻绳与电动机连接且轻绳拉直恰好无拉力,电动机的额定电压为$ U $,内阻为$ R $,正常工作时电流为$ I $,$ t = 0 $时刻启动电动机,使电动机在额定功率下拉动$ B $,$ t $时刻$ B $的速度达到最大,此时$ A $恰好离开墙壁,不计$ A $、$ B $间的静电力作用。求:

(1)物块$ B $的最大速度；
(2)弹簧的劲度系数。

答案： 2.答案：
(1)$\frac{UI - I^{2}R}{2qE}$
(2)$\frac{16q^{4}E^{4}}{8(UI - I^{2}R)tq^{2}E^{2} - m(UI - I^{2}R)^{2}}$
解析：
(1)当$B$的加速度$a = 0$时速度最大，此时轻绳上的拉力为$F = 2qE$
电动机的输出功率为$P = UI - I^{2}R$
又$P = Fv_{m}$
解得$v_{m} = \frac{UI - I^{2}R}{2qE}$。
(2)对$B$受力分析可知初始时刻弹簧弹力$F_{1} = qE$
$B$速度最大时弹簧弹力$F_{2} = qE$
所以从初始时刻到$B$速度最大的过程中，弹簧弹力对$B$做的总功为零
由动能定理得$Pt - 2qEx = \frac{1}{2}mv_{m}^{2}$
由胡克定律得$qE = kx$
联立解得$k = \frac{16q^{4}E^{4}}{8(UI - I^{2}R)tq^{2}E^{2} - m(UI - I^{2}R)^{2}}$。