2026年学易优高考二轮总复习物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(2025·山东泰安市二轮检测)用如图所示的装置探究加速度与力和质量的关系,带滑轮的长木板水平放置,弹簧测力计固定在墙上。小车上固定一定滑轮,细绳通过滑轮连接弹簧测力计和沙桶。

(1)实验时,一定要满足的条件或必要的操作是
A. 平衡摩擦力
B. 小车的质量远大于沙桶和沙的质量
(2)在实验中,有同学得到一条打点的纸带,取打点清晰部分做如下标记,如图甲所示,已知相邻计数点间还有4个点未画出,打点计时器的电源频率为50 Hz,则小车加速度的大小为$ a = $
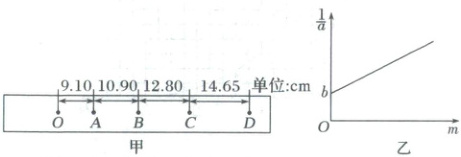
(3)在验证加速度与质量的关系时,在满足实验要求的情况下,改变小车上砝码质量$ m $,测出对应的加速度$ a $,以$ m $为横坐标,以$ \dfrac{1}{a} $为纵坐标,在坐标纸上作出如图乙所示的图像.已知弹簧测力计的读数为$ F $,图中纵轴的截距为$ b $,则小车的质量为

(1)实验时,一定要满足的条件或必要的操作是
A
;A. 平衡摩擦力
B. 小车的质量远大于沙桶和沙的质量
(2)在实验中,有同学得到一条打点的纸带,取打点清晰部分做如下标记,如图甲所示,已知相邻计数点间还有4个点未画出,打点计时器的电源频率为50 Hz,则小车加速度的大小为$ a = $
1.86
$ \mathrm{m/s^2} $(结果保留3位有效数字);
(3)在验证加速度与质量的关系时,在满足实验要求的情况下,改变小车上砝码质量$ m $,测出对应的加速度$ a $,以$ m $为横坐标,以$ \dfrac{1}{a} $为纵坐标,在坐标纸上作出如图乙所示的图像.已知弹簧测力计的读数为$ F $,图中纵轴的截距为$ b $,则小车的质量为
2Fb
。
答案:
答案:
(1)A
(2)1.86
(3)2Fb
解析:
(1)用如题图所示的装置探究加速度、力和质量的关系实验时,必要的操作是要平衡摩擦力,由于绳子的拉力可以通过弹簧测力计读出,故不需要满足小车的质量远大于沙桶和沙的质量,A正确,B错误。
(2)小车加速度的大小a=$\frac{(x_{3}+x_{4})-(x_{1}+x_{2})}{4T^{2}}$
=$\frac{(12.80+14.65)-(9.10+10.90)}{4×(5×0.02)^{2}}×10^{-2} m/s^2$
=$1.86 m/s^2$。
(3)根据牛顿第二定律有$2F=(m+M)a$,整理得$\frac{1}{a}=\frac{1}{2F}m+\frac{M}{2F}$。则$\frac{1}{a}-m$图线的截距$b=\frac{M}{2F}$,所以小车的质量$M=2Fb$。
(1)A
(2)1.86
(3)2Fb
解析:
(1)用如题图所示的装置探究加速度、力和质量的关系实验时,必要的操作是要平衡摩擦力,由于绳子的拉力可以通过弹簧测力计读出,故不需要满足小车的质量远大于沙桶和沙的质量,A正确,B错误。
(2)小车加速度的大小a=$\frac{(x_{3}+x_{4})-(x_{1}+x_{2})}{4T^{2}}$
=$\frac{(12.80+14.65)-(9.10+10.90)}{4×(5×0.02)^{2}}×10^{-2} m/s^2$
=$1.86 m/s^2$。
(3)根据牛顿第二定律有$2F=(m+M)a$,整理得$\frac{1}{a}=\frac{1}{2F}m+\frac{M}{2F}$。则$\frac{1}{a}-m$图线的截距$b=\frac{M}{2F}$,所以小车的质量$M=2Fb$。
2.(2025·河北唐山市二模)一金属线材电阻未知且电阻分布不均匀,为了测量其阻值并将其截为阻值相等的两段,实验研究小组设计了如图所示电路,实验器材如下:

未知电阻,阻值约为$ 4.8\ \Omega $;
微安表(零刻度在表盘中间),一端接导线,另一端接表笔;
定值电阻$ R_1 $,阻值为$ 10\ \Omega $;
电阻箱$ R_2 $,阻值$ 0\sim99.9\ \Omega $;
电流表,量程$ 0\sim0.6\ \mathrm{A} $,内阻$ R_{\mathrm{A}} = 1\ \Omega $;
电压表,量程$ 0\sim3.0\ \mathrm{V} $,内阻约为$ 3000\ \Omega $;
滑动变阻器,$ 0\sim10\ \Omega $;
电源,电动势为$ 3\ \mathrm{V} $;
开关,导线若干。
实验过程如下:
(1)按图连接电路,闭合开关之前,将滑动变阻器的滑片滑到最
(2)将电阻箱$ R_2 $的阻值调整到
(3)将滑动变阻器$ R_3 $的滑片调节到合适位置,连接微安表的表笔与未知电阻试触,防止微安表电流过大,不断改变表笔在未知电阻上的接触位置,直到
(4)保持表笔与记录的接触位置的接触,读出此时电流表和电压表的读数分别为

(5)通过两表读数可以得到未知电阻的阻值为

未知电阻,阻值约为$ 4.8\ \Omega $;
微安表(零刻度在表盘中间),一端接导线,另一端接表笔;
定值电阻$ R_1 $,阻值为$ 10\ \Omega $;
电阻箱$ R_2 $,阻值$ 0\sim99.9\ \Omega $;
电流表,量程$ 0\sim0.6\ \mathrm{A} $,内阻$ R_{\mathrm{A}} = 1\ \Omega $;
电压表,量程$ 0\sim3.0\ \mathrm{V} $,内阻约为$ 3000\ \Omega $;
滑动变阻器,$ 0\sim10\ \Omega $;
电源,电动势为$ 3\ \mathrm{V} $;
开关,导线若干。
实验过程如下:
(1)按图连接电路,闭合开关之前,将滑动变阻器的滑片滑到最
右
(填“左”或“右”)端;(2)将电阻箱$ R_2 $的阻值调整到
10
$ \Omega $,闭合开关;(3)将滑动变阻器$ R_3 $的滑片调节到合适位置,连接微安表的表笔与未知电阻试触,防止微安表电流过大,不断改变表笔在未知电阻上的接触位置,直到
流过微安表的电流为零
时,记录此次接触点的位置,即为等分电阻的位置;(4)保持表笔与记录的接触位置的接触,读出此时电流表和电压表的读数分别为
0.50
$ \mathrm{A} $和2.50
$ \mathrm{V} $;
(5)通过两表读数可以得到未知电阻的阻值为
6.7
$ \Omega $。
答案:
答案:
(1)右
(2)10
(3)流过微安表的电流为零
(4)0.50 2.50
(5)6.7
解析:
(1)按题图连接电路,闭合开关之前,要保护电路,让电流最小,则应将滑动变阻器的滑片滑到最右端,让阻值最大。
(2)由于为了测量其阻值并将其截为阻值相等的两段,则将电阻箱$R_2$的阻值调整为与定值电阻$R_1$相等,调为$10 \Omega$。
(3)利用了串联电阻的分压作用,当两电阻阻值相等时,电势降低一样,则两触点的电势相等,流过微安表的电流为零,所以为了等分电阻,只需要调节表笔在未知电阻上的接触位置,直到流过微安表的电流为零时,记录此次接触点的位置,即为等分电阻的位置。
(4)电流表的最小刻度为$0.02$ A,读数时,只需要同位估读,所以电流表的读数为$0.50$ A。 电压表的最小刻度为$0.1$ V,读数时,需要估读到下一位,所以电压表的读数为$2.50$ V。
(5)并联电阻的阻值为$R_{并}=\frac{U}{I}=\frac{2.50}{0.50} \Omega=5 \Omega$,
根据并联电路电阻关系有$\frac{1}{R_{并}}=\frac{1}{R_{x}}+\frac{1}{R_{1}+R_{2}}$,
代入数据解得$R_{x}=6.7 \Omega$。
(1)右
(2)10
(3)流过微安表的电流为零
(4)0.50 2.50
(5)6.7
解析:
(1)按题图连接电路,闭合开关之前,要保护电路,让电流最小,则应将滑动变阻器的滑片滑到最右端,让阻值最大。
(2)由于为了测量其阻值并将其截为阻值相等的两段,则将电阻箱$R_2$的阻值调整为与定值电阻$R_1$相等,调为$10 \Omega$。
(3)利用了串联电阻的分压作用,当两电阻阻值相等时,电势降低一样,则两触点的电势相等,流过微安表的电流为零,所以为了等分电阻,只需要调节表笔在未知电阻上的接触位置,直到流过微安表的电流为零时,记录此次接触点的位置,即为等分电阻的位置。
(4)电流表的最小刻度为$0.02$ A,读数时,只需要同位估读,所以电流表的读数为$0.50$ A。 电压表的最小刻度为$0.1$ V,读数时,需要估读到下一位,所以电压表的读数为$2.50$ V。
(5)并联电阻的阻值为$R_{并}=\frac{U}{I}=\frac{2.50}{0.50} \Omega=5 \Omega$,
根据并联电路电阻关系有$\frac{1}{R_{并}}=\frac{1}{R_{x}}+\frac{1}{R_{1}+R_{2}}$,
代入数据解得$R_{x}=6.7 \Omega$。
查看更多完整答案,请扫码查看


