2026年学易优高考二轮总复习物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. (多选)(2025·重庆模拟)两平行、光滑的直导轨与水平面间的夹角为$ \theta $,导轨处在垂直导轨平面向下的匀强磁场中,材料相同的匀质金属棒$ P、Q $垂直地放在导轨上,金属棒$ P $被直导轨上、与导轨平面垂直的两挡板(图中未画出)挡住,一根与导轨平行的轻质细绳跨过如图所示的轻质定滑轮,一端悬吊一重物,另一端连接金属棒$ Q $,将金属棒$ Q $由静止释放,经过一段时间后,金属棒$ Q $的速度始终为$ v $,金属棒$ P $与挡板间恰好无弹力作用。已知金属棒$ Q $的质量为$ 2m $,金属棒$ P $和重物的质量均为$ m $,金属棒运动过程中始终与导轨垂直并接触良好,直导轨电阻不计,重力加速度大小为$ g $,下列说法正确的是(
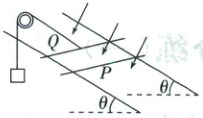
A.金属棒$ Q $运动过程中最大安培力为$ mg\sin\theta $
B.夹角$ \theta $的正弦值$ \sin\theta = \frac{1}{3} $
C.金属棒$ Q $的最大加速度为$ \frac{1}{9}g $
D.金属棒$ P $上产生的焦耳热的最大功率为$ \frac{1}{3}mgv $
ABC
)
A.金属棒$ Q $运动过程中最大安培力为$ mg\sin\theta $
B.夹角$ \theta $的正弦值$ \sin\theta = \frac{1}{3} $
C.金属棒$ Q $的最大加速度为$ \frac{1}{9}g $
D.金属棒$ P $上产生的焦耳热的最大功率为$ \frac{1}{3}mgv $
答案:
6.答案:ABC
解析:经过一段时间后金属棒Q的速度始终为v,即达到最大速度做匀速直线运动,此时金属棒P与挡板间恰好无弹力作用,则对金属棒P受力分析,可得安培力大小为$F_{安}=mg\sin\theta$,故A正确;对金属棒Q受力分析,有$F_{T}=2mg\sin\theta+F_{安}$,对重物有$F_{T}=mg$,联立解得$\sin\theta=\frac{1}{3}$,故B正确;金属棒Q刚运动时,加速度最大,对重物和Q连接体分析可得$mg-2mg\sin\theta=3ma_{max}$,解得最大加速度为$a_{max}=\frac{g}{9}$,故C正确;匀速时系统重力势能减少的功率为$mgv-2mg\sin\theta· v=\frac{1}{3}mgv$,由能量守恒定律知,回路焦耳热功率为$\frac{mgv}{3}$,故D错误。
解析:经过一段时间后金属棒Q的速度始终为v,即达到最大速度做匀速直线运动,此时金属棒P与挡板间恰好无弹力作用,则对金属棒P受力分析,可得安培力大小为$F_{安}=mg\sin\theta$,故A正确;对金属棒Q受力分析,有$F_{T}=2mg\sin\theta+F_{安}$,对重物有$F_{T}=mg$,联立解得$\sin\theta=\frac{1}{3}$,故B正确;金属棒Q刚运动时,加速度最大,对重物和Q连接体分析可得$mg-2mg\sin\theta=3ma_{max}$,解得最大加速度为$a_{max}=\frac{g}{9}$,故C正确;匀速时系统重力势能减少的功率为$mgv-2mg\sin\theta· v=\frac{1}{3}mgv$,由能量守恒定律知,回路焦耳热功率为$\frac{mgv}{3}$,故D错误。
7. (2025·四川内江模拟)某实验小组利用如图所示的实验装置来测量橡皮绳的劲度系数$ k $。将手机悬挂在橡皮绳下,用手机软件中的位移传感器可以测量手机在竖直方向上的位移。该实验小组进行了如下主要的实验步骤:
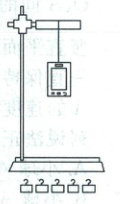
a. 将橡皮绳分别与手机和铁架台相连接,使手机重心和橡皮绳在同一竖直线上;
b. 用手掌托着手机,使橡皮绳处于原长状态,打开手机中的位移传感器软件;
c. 缓慢释放手机,当手机平衡时记录下手机下降的高度$ x_0 $;
d. 在手机正下方悬挂不同个数的钩码,每个钩码的质量$ m = 50\ g $,缓慢释放,当钩码平衡时,记录下从橡皮绳原长开始下降的伸长量$ x $;
e. 重复上述$ d $步操作;
f. 作出悬挂钩码数量$ n $及对应手机从橡皮绳原长开始下降的伸长量$ x $的关系图像,如图所示。
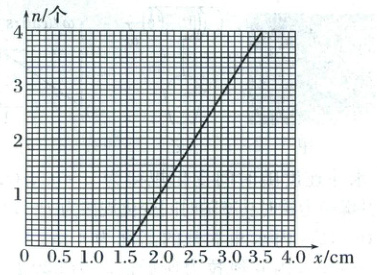
根据$ n - x $图像,回答以下问题:
(1)不挂钩码时,橡皮绳的伸长量为$ x_0 = $
(2)钩码个数$ n $与橡皮绳从原长开始下降的伸长量$ x $之间的函数关系式为$ n = $
(3)该橡皮绳的劲度系数$ k = $

a. 将橡皮绳分别与手机和铁架台相连接,使手机重心和橡皮绳在同一竖直线上;
b. 用手掌托着手机,使橡皮绳处于原长状态,打开手机中的位移传感器软件;
c. 缓慢释放手机,当手机平衡时记录下手机下降的高度$ x_0 $;
d. 在手机正下方悬挂不同个数的钩码,每个钩码的质量$ m = 50\ g $,缓慢释放,当钩码平衡时,记录下从橡皮绳原长开始下降的伸长量$ x $;
e. 重复上述$ d $步操作;
f. 作出悬挂钩码数量$ n $及对应手机从橡皮绳原长开始下降的伸长量$ x $的关系图像,如图所示。

根据$ n - x $图像,回答以下问题:
(1)不挂钩码时,橡皮绳的伸长量为$ x_0 = $
1.5 cm
$ cm $;(2)钩码个数$ n $与橡皮绳从原长开始下降的伸长量$ x $之间的函数关系式为$ n = $
\frac{k}{mg}x-\frac{kx_{0}}{mg}
(用字母$ k、x、x_0、m、g $表示);(3)该橡皮绳的劲度系数$ k = $
100
$ N/m(g = 10\ m/s^2) $。
答案:
7.答案:
(1)$1.5\ cm$
(2)$\frac{k}{mg}x-\frac{kx_{0}}{mg}$
(3)100
解析:
(1)根据题图可知不挂钩码时,橡皮绳的伸长量为$x_{0}=1.5\ cm$。
(2)根据胡克定律,有$nmg=k(x-x_{0})$
整理得$n=\frac{k}{mg}x-\frac{kx_{0}}{mg}$。
(3)由题图可知,图线的斜率为$k'=200\ m^{-1}$,该橡皮绳的劲度系数$k=k'mg=100\ N/m$。
(1)$1.5\ cm$
(2)$\frac{k}{mg}x-\frac{kx_{0}}{mg}$
(3)100
解析:
(1)根据题图可知不挂钩码时,橡皮绳的伸长量为$x_{0}=1.5\ cm$。
(2)根据胡克定律,有$nmg=k(x-x_{0})$
整理得$n=\frac{k}{mg}x-\frac{kx_{0}}{mg}$。
(3)由题图可知,图线的斜率为$k'=200\ m^{-1}$,该橡皮绳的劲度系数$k=k'mg=100\ N/m$。
8. 用某透明材料制作的半球形光学元件如图所示,平行单色光垂直射到半径为$ R $的半球底平面上,材料对该单色光的折射率$ n = \frac{5}{3} $,半球的上方平行于半球底平面放置一足够大的光屏,单色光经半球折射后在光屏上可形成一个圆形光斑。不考虑光的干涉、衍射及在半球内的多次反射,真空中光速为$ c $。求:
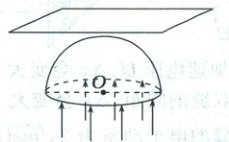
(1)当以临界角入射时,光线汇集点到$ O $点的距离;
(2)圆心$ O $到光屏的距离$ d = \frac{5}{2}R $时,光屏被照亮的面积。

(1)当以临界角入射时,光线汇集点到$ O $点的距离;
(2)圆心$ O $到光屏的距离$ d = \frac{5}{2}R $时,光屏被照亮的面积。
答案:
8.答案:
(1)$\frac{5}{4}R$
(2)$\frac{25}{9}\piR^{2}$
解析:
(1)作出剖面图如图所示,

光线入射到D点时恰好发生全反射,则有$\sin C=\frac{1}{n}$
由几何关系可得$OF=\frac{R}{\cos C}=\frac{R}{\sqrt{n^{2}-1}}=\frac{5}{4}R$。
(2)由图可得$\frac{O'F}{r}=\tan C$
$O'F=d-OF=\frac{5}{2}R-\frac{5}{4}R=\frac{5}{4}R$
解得$r=\frac{5}{3}R$
光屏被照亮的面积$S=\pi r^{2}=\pi(\frac{5}{3}R)^{2}=\frac{25}{9}\piR^{2}$。
8.答案:
(1)$\frac{5}{4}R$
(2)$\frac{25}{9}\piR^{2}$
解析:
(1)作出剖面图如图所示,

光线入射到D点时恰好发生全反射,则有$\sin C=\frac{1}{n}$
由几何关系可得$OF=\frac{R}{\cos C}=\frac{R}{\sqrt{n^{2}-1}}=\frac{5}{4}R$。
(2)由图可得$\frac{O'F}{r}=\tan C$
$O'F=d-OF=\frac{5}{2}R-\frac{5}{4}R=\frac{5}{4}R$
解得$r=\frac{5}{3}R$
光屏被照亮的面积$S=\pi r^{2}=\pi(\frac{5}{3}R)^{2}=\frac{25}{9}\piR^{2}$。
查看更多完整答案,请扫码查看


