《2026年学易优高考二轮总复习物理》

1. 某小组探究“法拉第圆盘发电机与电动机的功用”，设计了如图所示装置。飞轮由三根长$ a = 0.8\ m $的辐条和金属圆环组成，可绕过其中心的水平固定轴转动，不可伸长细绳绕在圆环上，系着质量$ m = 1\ kg $的物块，细绳与圆环无相对滑动。飞轮处在方向垂直环面的匀强磁场中，左侧电路通过电刷与转轴和圆环边缘良好接触，开关$ S $可分别与图示中的电路连接。已知电源电动势$ E_0 = 12\ V $、内阻$ r = 0.1\ \Omega $，限流电阻$ R_1 = 0.3\ \Omega $，飞轮每根辐条电阻$ R = 0.9\ \Omega $，电路中还有可调电阻$ R_2 $（待求）和电感线圈$ L $，不计其他电阻和阻力损耗，不计飞轮转轴大小。

(1) 开关$ S $掷$ 1 $，“电动机”提升物块匀速上升时，理想电压表示数$ U = 8\ V $；
① 判断磁场方向，并求流过电阻$ R_1 $的电流$ I $；
② 求物块匀速上升的速度$ v $；
(2) 开关$ S $掷$ 2 $，物块从静止开始下落，经过一段时间后，物块匀速下降的速度与“电动机”匀速提升物块的速度大小相等。
① 求可调电阻$ R_2 $的阻值；
② 求磁感应强度$ B $的大小。

答案：
1.答案:
(1)①垂直纸面向外　10A　②5m/s　
(2)①0.2Ω②2.5T
解析:
(1)①根据题意可知，飞轮逆时针转动，根据电路特点可知，三根辐条中的电流均沿辐条指向圆心，如图所示，根据左手定则可知，磁场方向垂直纸面向外
由于电压表示数U = 8V，则电源内阻与限流电阻的总分压为$U_{总}=E - U = 4V$
根据欧姆定律得$I=\frac{U_{总}}{r + R_{1}} = 10A$。

②根据能量守恒定律有$UIt = I^{2}· \frac{R}{3}t + mgvt$
代入数据解得$v = 5m/s$。
(2)①根据题意可知，物块匀速下降的速度$v' = v = 5m/s$，且稳定时每根辐条中的电流与
(1)中的相同，则根据能量守恒定律有
$mgv't = I^{2}· \frac{R}{3}t + I^{2}R_{2}t$
代入数据解得$R_{2}=0.2Ω$。
②稳定时，重物重力的功率等于三根辐条克服安培力做功的总功率，则有$mgv' = 3B· \frac{I}{3}a· \frac{v'}{2}$
代入数据解得$B = 2.5T$。

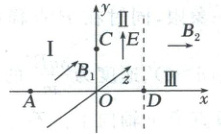
2. (2025·四川绵阳高三期末) 如图所示，$ Oxyz $为空间直角坐标系，在$ x ＜ 0 $的空间Ⅰ内存在沿$ z $轴正方向的匀强磁场$ B_1 $。在$ 0 ＜ x ＜ d $的空间Ⅱ内存在沿$ y $轴正方向的匀强电场$ E $，在$ x ＞ d $的空间Ⅲ内存在磁感应强度大小$ B_2 = \dfrac{mv_0}{qd} $、方向沿$ x $轴正方向的匀强磁场。现将一带负电的粒子从$ x $轴上的$ A(x_A = -\sqrt{3}d) $点以沿$ Oxy $平面内某一方向的初速度$ v_0 $射入空间Ⅰ的磁场区域，经磁场偏转后从$ y $轴上的$ C(y_C = d) $点垂直$ y $轴进入空间Ⅱ，并从$ x $轴上的$ D(x_D = d) $点进入空间Ⅲ。已知粒子的电荷量大小为$ q $，质量为$ m $，不计重力。求：

(1) 空间Ⅰ内磁场的磁感应强度大小$ B_1 $和空间Ⅱ内电场的电场强度大小$ E $；
(2) 粒子在空间Ⅲ的运动过程中，距离$ x $轴的最大距离；
(3) 粒子进入空间Ⅲ后，每次经过$ x $轴时的横坐标。

答案：
2.答案:
(1)$\frac{mv_{0}}{2qd}$　$\frac{2mv_{0}^{2}}{qd}$　
(2)4d　
(3)$(2n\pi + 1)d(n = 1,2,3,·s)$
解析:
(1)设粒子在空间I的磁场中的轨迹半径为$r_{1}$，运动轨迹如图所示。
由几何关系可得$(r_{1}-d)^{2}+(\sqrt{3}d)^{2}=r_{1}^{2}$
解得$r_{1}=2d$
由洛伦兹力提供向心力可得$qv_{0}B_{1}=m\frac{v_{0}^{2}}{r_{1}}$
解得$B_{1}=\frac{mv_{0}}{2qd}$
粒子在空间II做类平抛运动，沿y轴方向的加速度大小$a = \frac{qE}{m}$
沿x轴方向有$d = v_{0}t$
沿y轴方向有$d = \frac{1}{2}at^{2}$
解得$E=\frac{2mv_{0}^{2}}{qd}$。

(2)粒子经过D点时，沿y轴负方向的分速度大小为$v_{y}=at = 2v_{0}$
沿x轴正方向的分速度大小为$v_{x}=v_{0}$
粒子在空间III内垂直于磁场的分速度$v_{y}$使粒子在$yOz$平面内做匀速圆周运动，由洛伦兹力提供向心力可得$qv_{y}B_{2}=m\frac{v_{y}^{2}}{r_{2}}$
解得$r_{2}=2d$
粒子做圆周运动距x轴的最大距离为$L = 2r_{2}=4d$。
(3)粒子在空间III内做圆周运动的周期为$T=\frac{2\pi m}{qB_{2}}=\frac{2\pi d}{v_{0}}$
粒子在空间III内沿x轴方向做匀速直线运动，粒子在一个周期内沿x轴正方向运动的距离$x = v_{0}T = 2\pi d$
所以粒子在空间III中每次经过x轴时的横坐标为
$x = d + 2n\pi d=(2n\pi + 1)d(n = 1,2,3,·s)$。