2026年学易优高考二轮总复习物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. (2025·河南许昌市高考冲刺)开普勒186F是人们迄今发现的最像地球的一颗行星,这颗行星位于天鹅座开普勒186红外星5颗行星中的最外层,与恒星距离为5240万公里,距离地球约500光年。根据观测发现某颗行星(下文称为A星球)有一颗近地卫星,当地球的近地卫星转了4圈时,A星球的近地卫星才转了一圈,A星球的半径约为地球半径的$\frac{1}{4}$,设地球和A星球的密度、表面的重力加速度分别用$\rho_1$、$\rho_2$、$g_1$、$g_2$表示。则下列说法正确的是()
A.地球和A星球的密度之比$\rho_1 : \rho_2 = 1 : 16$
B.地球和A星球表面的重力加速度之比$g_1 : g_2 = 64 : 1$
C.分别在地球和A星球表面相同高度处以相同的速度平抛一个物体,A星球上的物体落地较早
D.A星球的自转角速度增加到$\omega = \sqrt{\frac{g_1}{128R_1}}$($R_1$为地球半径)时,会发生解体
A.地球和A星球的密度之比$\rho_1 : \rho_2 = 1 : 16$
B.地球和A星球表面的重力加速度之比$g_1 : g_2 = 64 : 1$
C.分别在地球和A星球表面相同高度处以相同的速度平抛一个物体,A星球上的物体落地较早
D.A星球的自转角速度增加到$\omega = \sqrt{\frac{g_1}{128R_1}}$($R_1$为地球半径)时,会发生解体
答案:
6.答案:B
解析:由题意可知$4T_1 = T_2$,$R_2 = \frac{1}{4} R_1$,对于近地卫星,在星球表面有$G \frac{Mm}{R^2} = m \frac{4\pi^2}{T^2} R$,星球的体积为$V = \frac{4}{3} \pi R^3$,星球的密度为$\rho = \frac{M}{V} = \frac{3\pi}{GT^2}$,故地球和A星球的密度之比$\rho_1 : \rho_2 = T_2^2 : T_1^2 = 16 : 1$,故A错误;对于近地卫星,在星球表面有$G \frac{Mm}{R^2} = mg$,地球和A星球表面的重力加速度之比$g_1 : g_2 = R_1 T_2^2 : R_2 T_1^2 = 64 : 1$,故B正确;物体做平抛运动有$h = \frac{1}{2} g t^2$,物体落地的时间$t = \sqrt{\frac{2h}{g}}$,A星球表面的重力加速度小,物体落地的时间较长,A星球上的物体落地较晚,故C错误;设A星球最外端的一物体质量为$m_0$,当角速度为$\omega$时,该物体将要离开A星球,即$G \frac{Mm_0}{R_2^2} = m_0 g_2 = m_0 \omega^2 R_2$,解得$\omega = \sqrt{\frac{g_2}{R_2}} = \sqrt{\frac{g_1}{16R_1}}$,故D错误。
解析:由题意可知$4T_1 = T_2$,$R_2 = \frac{1}{4} R_1$,对于近地卫星,在星球表面有$G \frac{Mm}{R^2} = m \frac{4\pi^2}{T^2} R$,星球的体积为$V = \frac{4}{3} \pi R^3$,星球的密度为$\rho = \frac{M}{V} = \frac{3\pi}{GT^2}$,故地球和A星球的密度之比$\rho_1 : \rho_2 = T_2^2 : T_1^2 = 16 : 1$,故A错误;对于近地卫星,在星球表面有$G \frac{Mm}{R^2} = mg$,地球和A星球表面的重力加速度之比$g_1 : g_2 = R_1 T_2^2 : R_2 T_1^2 = 64 : 1$,故B正确;物体做平抛运动有$h = \frac{1}{2} g t^2$,物体落地的时间$t = \sqrt{\frac{2h}{g}}$,A星球表面的重力加速度小,物体落地的时间较长,A星球上的物体落地较晚,故C错误;设A星球最外端的一物体质量为$m_0$,当角速度为$\omega$时,该物体将要离开A星球,即$G \frac{Mm_0}{R_2^2} = m_0 g_2 = m_0 \omega^2 R_2$,解得$\omega = \sqrt{\frac{g_2}{R_2}} = \sqrt{\frac{g_1}{16R_1}}$,故D错误。
7. (2025·黑龙江哈尔滨二模)质量为$m$的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上。平衡时,弹簧的压缩量为$x_0$,如图所示,一质量为$2m$的物块从钢板正上方距离为$4.5x_0$的$A$处自由落下,打在钢板上并立刻与钢板粘连一起向下运动。它们到达最低点后又向上运动。已知弹簧以原长处为零势能面的弹性势能表达式为$E_p = \frac{1}{2}kx^2$,弹簧振子做简谐运动的周期$T = 2\pi\sqrt{\frac{M}{k}}$,($x$为弹簧形变量,$M$为振子的质量,$k$为弹簧劲度系数),钢板与物块均可视为质点,弹簧始终在弹性限度内,重力加速度为$g$,下列说法正确的是()
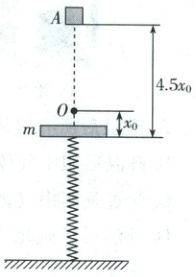
A.物块与钢板碰撞后一起下落的初速度是$3\sqrt{gx_0}$
B.碰后物块与钢板一起做简谐运动,振幅$A = 6x_0$
C.碰撞刚结束至两者第一次运动到最低点所经历的时间$t = \frac{2\pi}{3}\sqrt{\frac{3x_0}{g}}$
D.运动过程中弹簧的最大弹性势能$E_{pm} = 18mgx_0$

A.物块与钢板碰撞后一起下落的初速度是$3\sqrt{gx_0}$
B.碰后物块与钢板一起做简谐运动,振幅$A = 6x_0$
C.碰撞刚结束至两者第一次运动到最低点所经历的时间$t = \frac{2\pi}{3}\sqrt{\frac{3x_0}{g}}$
D.运动过程中弹簧的最大弹性势能$E_{pm} = 18mgx_0$
答案:
7.答案:C
解析:对物块,根据动能定理有$2mg · 4.5x_0 = \frac{1}{2} · 2m v_0^2$,解得$v_0 = \sqrt{3gx_0}$,设$v_1$表示质量为$2m$的物块与钢板碰撞后一起开始向下运动的速度,因碰撞时间极短,动量守恒,取$v_0$方向为正,则$2m v_0 = 3m v_1$,解得$v_1 = \frac{2v_0}{3} = 2 \sqrt{gx_0}$,故A错误;碰撞后根据能量守恒$\frac{1}{2} kx_0^2 + \frac{1}{2} × 3m v_1^2 + 3mg(x_1 - x_0) = \frac{1}{2} kx_1^2$,根据平衡条件可得$F_{弹} = kx_0 = mg$,解得$x_1 = 7x_0$,当物块与钢板受力平衡时,为平衡位置$3mg = kx_2$,解得$x_2 = 3x_0$,所以振幅为$A = x_1 - x_2 = 4x_0$,故B错误;碰撞刚结束至两者第一次运动到平衡位置时间为$t_1$,则$\sin \frac{2\pi t_1}{T} = \frac{2x_0}{A}$,解得$t_1 = \frac{T}{12}$,继续运动到最低点所经历的时间$t_2$,则$t_2 = \frac{T}{4}$,所以,碰撞刚结束至两者第一次运动到最低点所经历的时间$t = t_1 + t_2 = \frac{T}{3} - \frac{1}{3} × 2\pi \sqrt{\frac{3m}{k}} = \frac{2\pi}{3} \sqrt{\frac{3m}{g}}$,故C正确;当物块与钢板运动到最低点时,弹簧的弹性势能最大$E_{pm} = \frac{1}{2} kx_1^2 = 24.5mgx_0$,故D错误。
解析:对物块,根据动能定理有$2mg · 4.5x_0 = \frac{1}{2} · 2m v_0^2$,解得$v_0 = \sqrt{3gx_0}$,设$v_1$表示质量为$2m$的物块与钢板碰撞后一起开始向下运动的速度,因碰撞时间极短,动量守恒,取$v_0$方向为正,则$2m v_0 = 3m v_1$,解得$v_1 = \frac{2v_0}{3} = 2 \sqrt{gx_0}$,故A错误;碰撞后根据能量守恒$\frac{1}{2} kx_0^2 + \frac{1}{2} × 3m v_1^2 + 3mg(x_1 - x_0) = \frac{1}{2} kx_1^2$,根据平衡条件可得$F_{弹} = kx_0 = mg$,解得$x_1 = 7x_0$,当物块与钢板受力平衡时,为平衡位置$3mg = kx_2$,解得$x_2 = 3x_0$,所以振幅为$A = x_1 - x_2 = 4x_0$,故B错误;碰撞刚结束至两者第一次运动到平衡位置时间为$t_1$,则$\sin \frac{2\pi t_1}{T} = \frac{2x_0}{A}$,解得$t_1 = \frac{T}{12}$,继续运动到最低点所经历的时间$t_2$,则$t_2 = \frac{T}{4}$,所以,碰撞刚结束至两者第一次运动到最低点所经历的时间$t = t_1 + t_2 = \frac{T}{3} - \frac{1}{3} × 2\pi \sqrt{\frac{3m}{k}} = \frac{2\pi}{3} \sqrt{\frac{3m}{g}}$,故C正确;当物块与钢板运动到最低点时,弹簧的弹性势能最大$E_{pm} = \frac{1}{2} kx_1^2 = 24.5mgx_0$,故D错误。
8. 如图所示,为一个水平弹簧振子的振动图像,下列说法正确的是()

A.$t = 1\ s$到$t = 2\ s$内,弹簧振子的动能不断减小
B.该弹簧振子的振动方程为$x = -10\sin\left(\frac{\pi}{2}t\right)\ cm$
C.$t = 3\ s$时,弹簧振子的加速度沿$x$轴负方向
D.$t = 0$到$t = 10\ s$内弹簧振子的路程为$50\ cm$

A.$t = 1\ s$到$t = 2\ s$内,弹簧振子的动能不断减小
B.该弹簧振子的振动方程为$x = -10\sin\left(\frac{\pi}{2}t\right)\ cm$
C.$t = 3\ s$时,弹簧振子的加速度沿$x$轴负方向
D.$t = 0$到$t = 10\ s$内弹簧振子的路程为$50\ cm$
答案:
8.答案:BC
解析:$t = 1 s$到$t = 2 s$内,弹簧振子从最大位移处向平衡位置运动,则振子的动能不断增加,故A错误;因为$\omega = \frac{2\pi}{T} = \frac{\pi}{2} rad/s$,振幅$A = 10 cm$,该弹簧振子的振动方程为$x = -10 \sin (\frac{\pi}{2} t) cm$,故B正确;$t = 3 s$时,弹簧振子的位移正向最大,则加速度沿$x$轴负方向,故C正确;因$10 s = 2.5T$,则$t = 0$到$t = 10 s$内弹簧振子的路程为$2.5 × 4A = 100 cm$,故D错误。
解析:$t = 1 s$到$t = 2 s$内,弹簧振子从最大位移处向平衡位置运动,则振子的动能不断增加,故A错误;因为$\omega = \frac{2\pi}{T} = \frac{\pi}{2} rad/s$,振幅$A = 10 cm$,该弹簧振子的振动方程为$x = -10 \sin (\frac{\pi}{2} t) cm$,故B正确;$t = 3 s$时,弹簧振子的位移正向最大,则加速度沿$x$轴负方向,故C正确;因$10 s = 2.5T$,则$t = 0$到$t = 10 s$内弹簧振子的路程为$2.5 × 4A = 100 cm$,故D错误。
9. 如图所示,某次用白球击打静止的蓝球,两球碰后沿同一直线运动。蓝球经$t = 0.6\ s$的时间向前运动$x_1 = 0.36\ m$刚好(速度为0)落入袋中,而白球沿同一方向运动$x_2 = 0.16\ m$停止运动,已知两球的质量相等,碰后以相同的加速度做匀变速直线运动,假设两球碰撞的时间极短且发生正碰(内力远大于外力),则下列说法正确的是()

A.由于摩擦不能忽略,则碰撞过程动量不守恒
B.碰后蓝球与白球的速度之比为$3:2$
C.碰撞前白球的速度大小为$2\ m/s$
D.该碰撞为弹性碰撞

A.由于摩擦不能忽略,则碰撞过程动量不守恒
B.碰后蓝球与白球的速度之比为$3:2$
C.碰撞前白球的速度大小为$2\ m/s$
D.该碰撞为弹性碰撞
答案:
9.答案:BC
解析:由题意可知两球碰撞的时间极短,碰撞过程中产生极大的内力,两球与桌面间的摩擦力远远小于内力,所以该碰撞过程动量守恒,故A错误;碰后蓝球与白球均做匀减速直线运动,两球的加速度大小相等,由公式$v^2 = 2ax$得$\frac{v_1}{v_2} = \sqrt{\frac{x_1}{x_2}} = \frac{3}{2}$,则碰后蓝球与白球的速度大小之比为$3 : 2$,故B正确;碰撞后蓝球速度$v_1 = \frac{2x_1}{t} = 1.2 m/s$,白球速度$v_2 = \frac{2}{3} v_1 = 0.8 m/s$,碰撞过程中两球组成的系统动量守恒,则$mv_0 = mv_1 + mv_2$,代入数据解得$v_0 = 2 m/s$,故C正确;两球碰前的动能为$E_{k1} = \frac{1}{2} m v_0^2 = 2m$,两球碰后的总动能为$E_{k2} = \frac{1}{2} m v_1^2 + \frac{1}{2} m v_2^2 = 1.04m$,由于$E_{k1} > E_{k2}$,所以该碰撞过程有机械能损失,即该碰撞为非弹性碰撞,故D错误。
解析:由题意可知两球碰撞的时间极短,碰撞过程中产生极大的内力,两球与桌面间的摩擦力远远小于内力,所以该碰撞过程动量守恒,故A错误;碰后蓝球与白球均做匀减速直线运动,两球的加速度大小相等,由公式$v^2 = 2ax$得$\frac{v_1}{v_2} = \sqrt{\frac{x_1}{x_2}} = \frac{3}{2}$,则碰后蓝球与白球的速度大小之比为$3 : 2$,故B正确;碰撞后蓝球速度$v_1 = \frac{2x_1}{t} = 1.2 m/s$,白球速度$v_2 = \frac{2}{3} v_1 = 0.8 m/s$,碰撞过程中两球组成的系统动量守恒,则$mv_0 = mv_1 + mv_2$,代入数据解得$v_0 = 2 m/s$,故C正确;两球碰前的动能为$E_{k1} = \frac{1}{2} m v_0^2 = 2m$,两球碰后的总动能为$E_{k2} = \frac{1}{2} m v_1^2 + \frac{1}{2} m v_2^2 = 1.04m$,由于$E_{k1} > E_{k2}$,所以该碰撞过程有机械能损失,即该碰撞为非弹性碰撞,故D错误。
10. (2025·山东东营二模)如图所示,两水平虚线间存在垂直于纸面方向的匀强磁场,两虚线间的距离为$\frac{7}{4}h$,磁感应强度大小为$B$。边长为$h$的正方形导体框由虚线1上方无初速度释放,在释放瞬间$ab$边与虚线1平行且相距$h$。已知导体框的质量为$m$,总电阻为$r$,重力加速度为$g$,$ab$边与两虚线重合时的速度大小相等,忽略空气阻力,导体框在运动过程中不会发生转动,则()
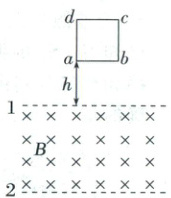
A.导体框可能先加速后减速
B.导体框在穿越磁场的过程中,产生的焦耳热为$4mgh$
C.导体框的最小速度是$v = \frac{\sqrt{2gh}}{2}$
D.导体框从$ab$边与虚线1重合到$cd$边与虚线1重合时所用的时间为$\frac{B^2h^3}{mgr} - \sqrt{\frac{h}{2g}}$

A.导体框可能先加速后减速
B.导体框在穿越磁场的过程中,产生的焦耳热为$4mgh$
C.导体框的最小速度是$v = \frac{\sqrt{2gh}}{2}$
D.导体框从$ab$边与虚线1重合到$cd$边与虚线1重合时所用的时间为$\frac{B^2h^3}{mgr} - \sqrt{\frac{h}{2g}}$
答案:
10.答案:CD
解析:已知$ab$边与两虚线重合时的速度大小相等,则导体框在$cd$边与虚线1重合时速度最小。设$ab$边与虚线1重合时速度为$v_1$,则有$v_1^2 = 2gh$,设$cd$边与虚线1重合时导体框的速度为$v_2$,$ab$边与虚线2重合时的速度为$v_3$,则有$v_3 = v_1 = \sqrt{2gh}$,$v_3^2 - v_2^2 = 2g × (\frac{7}{4}h - h)$,联立解得$v_2 = \frac{\sqrt{2gh}}{2}$,整个过程中导体框经历了先加速、后减速、再加速、再次减速,出磁场后做匀加速运动,故A错误,C正确;根据运动的对称性可知,导体框完全离开磁场时的速度为$v_4 = v_2 = \frac{\sqrt{2gh}}{2}$,根据能量守恒定律可得$mg(2h + \frac{7}{4}h) = \frac{1}{2} m v_4^2 + Q$,解得$Q = \frac{7}{2} mgh$,故B错误;设导体框从$ab$边与虚线1重合到$cd$边与虚线1重合时所用的时间为$t$,线框中的平均感应电流为$\overline{I}$,则由动量定理可得$mgt - B\overline{I}ht = mv_2 - mv_1$,流过导体某一截面的电荷量为$q = \overline{I}t = \frac{E}{r} t = \frac{Bh^2}{r}$,联立解得$t = \frac{B^2 h^3}{mgr} \sqrt{\frac{h}{2g}}$,故D正确。
解析:已知$ab$边与两虚线重合时的速度大小相等,则导体框在$cd$边与虚线1重合时速度最小。设$ab$边与虚线1重合时速度为$v_1$,则有$v_1^2 = 2gh$,设$cd$边与虚线1重合时导体框的速度为$v_2$,$ab$边与虚线2重合时的速度为$v_3$,则有$v_3 = v_1 = \sqrt{2gh}$,$v_3^2 - v_2^2 = 2g × (\frac{7}{4}h - h)$,联立解得$v_2 = \frac{\sqrt{2gh}}{2}$,整个过程中导体框经历了先加速、后减速、再加速、再次减速,出磁场后做匀加速运动,故A错误,C正确;根据运动的对称性可知,导体框完全离开磁场时的速度为$v_4 = v_2 = \frac{\sqrt{2gh}}{2}$,根据能量守恒定律可得$mg(2h + \frac{7}{4}h) = \frac{1}{2} m v_4^2 + Q$,解得$Q = \frac{7}{2} mgh$,故B错误;设导体框从$ab$边与虚线1重合到$cd$边与虚线1重合时所用的时间为$t$,线框中的平均感应电流为$\overline{I}$,则由动量定理可得$mgt - B\overline{I}ht = mv_2 - mv_1$,流过导体某一截面的电荷量为$q = \overline{I}t = \frac{E}{r} t = \frac{Bh^2}{r}$,联立解得$t = \frac{B^2 h^3}{mgr} \sqrt{\frac{h}{2g}}$,故D正确。
查看更多完整答案,请扫码查看


