《2026年学易优高考二轮总复习物理》

9. (2025·江西南昌模拟)一滑板训练场地如图,斜坡$ AB $与光滑圆轨道相切于$ B $点,斜坡长度为$ 10\ m $,倾角为$ 37° $,圆轨道半径为$ 3\ m $,圆心为$ O $,圆轨道右侧与一倾角为$ 60° $足够长斜面$ PQ $相连,运动员连同滑板总质量为$ 60\ kg $,运动员站在滑板上从斜坡顶端$ A $点由静止下滑,滑板与左侧倾斜轨道间的动摩擦因数为$ 0.2 $,其通过光滑圆弧轨道$ BCP $的$ P $点后落在了右侧的斜面上,滑板和人可视为质点,不计空气阻力,重力加速度$ g $取$ 10\ m/s^2 $,$ \sin37° = 0.6 $。求:

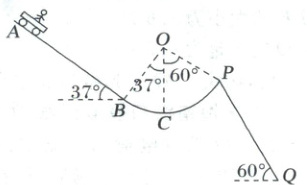
(1)滑板和人通过圆弧轨道最低点$ C $时对$ C $点的压力大小;
(2)滑块和人在右侧斜面的落点到$ P $点的距离。

答案： 9.答案:
(1)$2600\ N$
(2)$14\sqrt{3}\ m$
解析:
(1)对滑板和人从A点到C点，应用动能定理得
$mgL\sin37^{\circ}-\mu mgL\cos37^{\circ}+mgR(1-\cos37^{\circ})=\frac{1}{2}mv^{2}$
解得$v=10\ m/s$
在最低点C点，有$F_{N}-mg=m\frac{v^{2}}{R}$
求得$F_{N}=2600\ N$
由牛顿第三定律可得，滑板和人通过圆弧轨道最低点C时对C点的压力大小为$2600\ N$。
(2)从C到P应用动能定理可得
$-mgR(1-\cos60^{\circ})=\frac{1}{2}mv_{1}^{2}-\frac{1}{2}mv^{2}$
求得$v_{1}=\sqrt{70}\ m/s$
设滑板和人在右侧斜面的落点到P点的距离为$l$，由抛体运动规律可得
$l\cos60^{\circ}=v_{1}t$
$l\sin60^{\circ}=-v_{1y}t+\frac{1}{2}gt^{2}$
其中$v_{1x}=v_{1}\cos60^{\circ}$，$v_{1y}=v_{1}\sin60^{\circ}$
解得$l=14\sqrt{3}\ m$。

10. (2025·天津河西模拟预测)电动汽车通过能量回收装置增加电池续航。在行驶过程中,踩下驱动踏板时电池给电动机供电,松开驱动踏板或踩下刹车时发电机工作回收能量。某兴趣小组为研究其原理,设计了如图所示的模型:两个半径不同的同轴圆柱体间存在由内至外的辐向磁场,磁场方向沿半径方向,有一根质量为$ m $、长度为$ L $、电阻为$ R $的金属棒$ MN $通过导电轻杆与中心轴相连,可绕轴无摩擦转动,金属棒所在之处的磁感应强度大小均为$ B $,整个装置竖直方向放置。中心轴右侧接一单刀双掷开关:踩下驱动踏板,开关接通$ 1 $,电池给金属棒供电,金属棒相当于电动机,所用电池的电动势为$ E $,内阻为$ r $;松开驱动踏板或踩下刹车,开关自动切换接通$ 2 $,金属棒相当于发电机,给电容器充电,所接电容器电容为$ C $。初始时电容器不带电、金属棒$ MN $静止,电路其余部分的电阻不计。

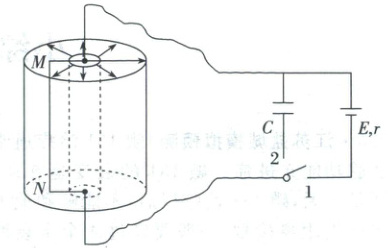
(1)踩下驱动踏板后,求金属棒刚启动时加速度$ a $的大小及开始运动后的转动方向(从上往下看);
(2)踩下驱动踏板后,求金属棒可达到的最大转动线速度;
(3)当金属棒达到最大转动速度后松开驱动踏板,在一段时间后金属棒$ MN $将匀速转动。
①求此时电容器$ C $上的带电荷量;
②定性画出松开驱动踏板后的电容器的电压与电荷量关系的$ U - q $图像,并结合图像和题目中的条件,求电容器最终能回收多少能量储存起来。

答案：
10．答案：
(1)$\frac{BEL}{m(R+r)}$，金属棒开始运动后沿顺时针转动
(2)$\frac{E}{BL}$
(3)①$\frac{mCE}{m+CB^{2}L^{2}}$ ②见解析，$\frac{Cm^{2}E^{2}}{2(B^{2}L^{2}C+m)^{2}}$
解析：
(1)电流方向向下，根据左手定则判断，从上往下看，金属棒开始运动后沿顺时针转动，当开关闭合的瞬间，金属棒还没有发生转动，则有$I=\frac{E}{R+r}$
金属棒在安培力作用下发生转动，根据牛顿第二定律有$BIL=ma$
解得$a=\frac{BEL}{m(R+r)}$。
(2)当金属棒达到最大线速度$v_{m}$时，金属棒中无电流通过，即金属棒切割磁感线产生的感应电动势大小为E，则有$E=BLv_{m}$
解得$v_{m}=\frac{E}{BL}$。
(3)①当金属棒由最大速度减速至匀速转动，由动量定理可得$-\sum BiL\Delta t=-BqL=mv-mv_{m}$
当电路达到稳定时，回路中无电流，电容器两端电压与金属棒切割产生的感应电动势相等，则有$\frac{q}{C}=BLv$
结合上述解得$q=\frac{mCE}{m+CB^{2}L^{2}}$。
②根据电容的定义式有$C=\frac{q}{U}$，则有$U=\frac{q}{C}$
作出U - q图像如图所示

由于$q=\frac{mCE}{m+CB^{2}L^{2}}$
由微元法可知图像下面积等于电容器储存的电能，则有$W=\frac{1}{2}Uq=\frac{q^{2}}{2C}=\frac{1}{2}CU^{2}$
结合上述解得$W=\frac{Cm^{2}E^{2}}{2(B^{2}L^{2}C+m)^{2}}$。