2026年学易优高考二轮总复习物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图所示,平面直角坐标系$xOy$中第一、二、四象限内存在磁感应强度大小为$B$的匀强磁场。第一、四象限内磁场方向垂直纸面向里,第二象限内磁场方向垂直纸面向外。第三象限存在沿$y$轴正方向的匀强电场。质量为$m$、电荷量为$q(q>0)$的粒子甲从点$S(-l,-\frac{l}{2})$以一定初速度释放,初速度方向与$x$轴正方向的夹角$\theta = 45^{\circ}$,从点$K(0,-l)$垂直$y$轴进入第四象限磁场区域,然后从$P(l,0)$点垂直$x$轴进入第一象限,同时在$P$点释放一质量为$\frac{m}{3}$、电荷量为$q(q>0)$、速度为$\frac{3qBl}{m}$的带电粒子乙,且速度方向垂直于$x$轴向上。不计粒子重力及甲、乙两粒子间的相互作用,求:
(1)甲粒子进入第四象限时的速度$v_{0}$;
(2)匀强电场的大小$E$;
(3)甲粒子第$n$次经过$y$轴时,甲、乙粒子间的距离$d$。
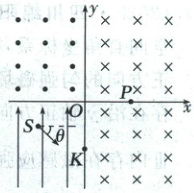
(1)甲粒子进入第四象限时的速度$v_{0}$;
(2)匀强电场的大小$E$;
(3)甲粒子第$n$次经过$y$轴时,甲、乙粒子间的距离$d$。

答案:
1.答案:
(1)$\frac{qBl}{m}$
(2)$\frac{qB^{2}l}{m}$
(3)(4n - 2)l(n = 1,2,3,...)
解析:
(1)甲粒子在第四象限内的磁场中,由洛伦兹力提供向心力$qv_{0}B = m\frac{v_{0}^{2}}{r}$
根据题意有$r = l$,解得$v_{0} = \frac{qBl}{m}$。
(2)由题意知甲粒子垂直$y$轴进入第四象限,速度大小为$v_{0} = \frac{qBl}{m}$
粒子在第三象限,沿$x$轴方向$l = v_{0}t_{0}$
沿$y$轴方向$\frac{l}{2} = \frac{1}{2}·\frac{qE}{m}t_{0}^{2}$
解得$E = \frac{qB^{2}l}{m}$
(3)设甲粒子半径为$r_{1}$,乙粒子半径为$r_{2}$
由洛伦兹力提供向心力得$qv_{0}B = m\frac{v_{0}^{2}}{r_{1}}$,$qv_{2}B = m\frac{v_{2}^{2}}{3r_{2}}$,其中$v_{2} = \frac{3qBl}{m}$
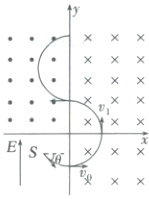
可得$r_{1} = r_{2} = l$
甲、乙粒子的周期分别为$T_{1} = \frac{2\pi r_{1}}{v_{0}}$,$T_{2} = \frac{2\pi r_{2}}{v_{2}}$
可得$T_{1} = 3T_{2}$
如图所示,当甲粒子第一次到达$y$轴($y_{1} = l$)时,乙粒子第二次到达$y$轴($y_{2} = 3l$),两粒子相距$d_{1} = 2l$
此后每次甲粒子到达$y$轴时,乙比甲沿$y$轴多移动$\Delta d = 4l$
粒子甲第$n$次经过$y$轴时甲、乙粒子间的距离$d = (4n - 2)l(n = 1,2,3,...)$。
1.答案:
(1)$\frac{qBl}{m}$
(2)$\frac{qB^{2}l}{m}$
(3)(4n - 2)l(n = 1,2,3,...)
解析:
(1)甲粒子在第四象限内的磁场中,由洛伦兹力提供向心力$qv_{0}B = m\frac{v_{0}^{2}}{r}$
根据题意有$r = l$,解得$v_{0} = \frac{qBl}{m}$。
(2)由题意知甲粒子垂直$y$轴进入第四象限,速度大小为$v_{0} = \frac{qBl}{m}$
粒子在第三象限,沿$x$轴方向$l = v_{0}t_{0}$
沿$y$轴方向$\frac{l}{2} = \frac{1}{2}·\frac{qE}{m}t_{0}^{2}$
解得$E = \frac{qB^{2}l}{m}$
(3)设甲粒子半径为$r_{1}$,乙粒子半径为$r_{2}$
由洛伦兹力提供向心力得$qv_{0}B = m\frac{v_{0}^{2}}{r_{1}}$,$qv_{2}B = m\frac{v_{2}^{2}}{3r_{2}}$,其中$v_{2} = \frac{3qBl}{m}$

可得$r_{1} = r_{2} = l$
甲、乙粒子的周期分别为$T_{1} = \frac{2\pi r_{1}}{v_{0}}$,$T_{2} = \frac{2\pi r_{2}}{v_{2}}$
可得$T_{1} = 3T_{2}$
如图所示,当甲粒子第一次到达$y$轴($y_{1} = l$)时,乙粒子第二次到达$y$轴($y_{2} = 3l$),两粒子相距$d_{1} = 2l$
此后每次甲粒子到达$y$轴时,乙比甲沿$y$轴多移动$\Delta d = 4l$
粒子甲第$n$次经过$y$轴时甲、乙粒子间的距离$d = (4n - 2)l(n = 1,2,3,...)$。
第二题
2. (2025·河北唐山二模)如图所示,粗糙水平地面上固定一个光滑斜面体,在斜面体末端紧靠一个足够长的薄木板$B$,均处于静止状态,薄木板$B$与斜面体末端等高且平滑连接,距离薄木板$B$的右端$0.5\ m$位置处静止放置一个物块$C$。已知物块$A$的质量为$2\ kg$,薄木板$B$和物块$C$的质量均为$1\ kg$,物块$A$与薄木板$B$之间的动摩擦因数为$0.2$,薄木板$B$和物块$C$与地面之间的动摩擦因数均为$0.1$,薄木板$B$和物块$C$的高度相同,运动过程中物块$A$始终不会滑离薄木板$B$,所有碰撞时间极短且均为弹性碰撞。物块$A$在距离薄木板$B$的上表面$1.8\ m$高处沿斜面体静止释放,$A$由斜面滑上薄木板$B$的过程中能量损失不计,重力加速度$g$取$10\ m/s^2$。求:
(1)薄木板$B$与物块$C$碰撞前,物块$A$速度大小是多少?
(2)薄木板$B$与物块$C$第一次碰撞到第二次碰撞经历的时间;
(3)最终停止时,薄木板$B$与物块$C$的距离。
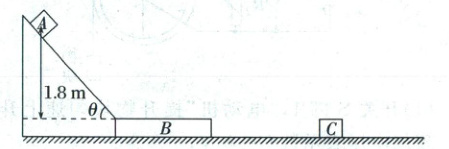
2. (2025·河北唐山二模)如图所示,粗糙水平地面上固定一个光滑斜面体,在斜面体末端紧靠一个足够长的薄木板$B$,均处于静止状态,薄木板$B$与斜面体末端等高且平滑连接,距离薄木板$B$的右端$0.5\ m$位置处静止放置一个物块$C$。已知物块$A$的质量为$2\ kg$,薄木板$B$和物块$C$的质量均为$1\ kg$,物块$A$与薄木板$B$之间的动摩擦因数为$0.2$,薄木板$B$和物块$C$与地面之间的动摩擦因数均为$0.1$,薄木板$B$和物块$C$的高度相同,运动过程中物块$A$始终不会滑离薄木板$B$,所有碰撞时间极短且均为弹性碰撞。物块$A$在距离薄木板$B$的上表面$1.8\ m$高处沿斜面体静止释放,$A$由斜面滑上薄木板$B$的过程中能量损失不计,重力加速度$g$取$10\ m/s^2$。求:
(1)薄木板$B$与物块$C$碰撞前,物块$A$速度大小是多少?
(2)薄木板$B$与物块$C$第一次碰撞到第二次碰撞经历的时间;
(3)最终停止时,薄木板$B$与物块$C$的距离。

答案:
2.答案:
(1)$4m/s$
(2)$1s$
(3)$\frac{1}{18}m$
解析:
(1)物块A到达木板时,设速度为$v_{0}$,由动能定理可得$m_{A}gh = \frac{1}{2}m_{A}v_{0}^{2}$
解得$v_{0} = 6m/s$
在B、C相碰之前,设物块A的速度$v_{1}$,加速度大小为$a_{A}$,木板B的速度为$v_{2}$,加速度为$a_{B}$,滑动时间为$t_{1}$
由牛顿第二定律可得$\mu_{1}m_{A}g = m_{A}a_{A}$
$\mu_{1}m_{A}g - \mu_{2}(m_{A} + m_{B})g = m_{B}a_{B}$
解得$a_{A} = 2m/s^{2}$,$a_{B} = 1m/s^{2}$
由运动学规律,对B:$x_{1} = \frac{1}{2}a_{B}t_{1}^{2}$
对A:$v_{1} = v_{0} - a_{A}t_{1}$
解得$v_{1} = 4m/s$,$v_{2} = a_{B}t_{1} = 1m/s$。
(2)木板B与物块C相碰,设碰后B、C的速度分别为$v_{3}$、$v_{4}$
由动量守恒定律和能量守恒定律可得$m_{B}v_{2} = m_{B}v_{3} + m_{C}v_{4}$
$\frac{1}{2}m_{B}v_{2}^{2} = \frac{1}{2}m_{B}v_{3}^{2} + \frac{1}{2}m_{C}v_{4}^{2}$
解得$v_{3} = 0$,$v_{4} = 1m/s$
碰后C做匀减速运动,设加速度大小为$a_{C}$,经历时间为$t_{3}$,位移为$x_{2}$,
则$\mu_{2}m_{C}g = m_{C}a_{C}$
解得$a_{C} = 1m/s^{2}$
第二次碰撞前C静止,则$v_{4} = a_{C}t_{3}$
解得时间为$t_{3} = 1s$
此时运动距离为$x_{2} = \frac{1}{2}a_{C}t_{3}^{2} = 0.5m$
由$x = \frac{1}{2}a_{B}t_{3}^{2}$知B在$1s$内恰好移动$0.5m$,B追上C,二者加速度大小相同,B加速,C减速,故所需时间为$1s$,即从第一次碰撞到第二次碰撞经历时间为$1s$。
(3)第二次碰撞后,设A的速度为$v_{5}$,由运动学规律可得$v_{5} = v_{1} - a_{A}t_{3}$
设木板与物块A达到共速时,速度为$v_{6}$,时间为$t_{4}$,则$v_{6} = v_{5} - a_{A}t_{4}$,$v_{6} = a_{B}t_{4}$
设木板共速之前的位移为$x_{3}$,共速之后的位移为$x_{4}$,
则$x_{3} = \frac{1}{2}a_{B}t_{4}^{2}$,$v_{6}^{2} = 2a_{B}x_{4}$,$x = x_{2} - x_{3} - x_{4}$,解得$x = \frac{1}{18}m$。
(1)$4m/s$
(2)$1s$
(3)$\frac{1}{18}m$
解析:
(1)物块A到达木板时,设速度为$v_{0}$,由动能定理可得$m_{A}gh = \frac{1}{2}m_{A}v_{0}^{2}$
解得$v_{0} = 6m/s$
在B、C相碰之前,设物块A的速度$v_{1}$,加速度大小为$a_{A}$,木板B的速度为$v_{2}$,加速度为$a_{B}$,滑动时间为$t_{1}$
由牛顿第二定律可得$\mu_{1}m_{A}g = m_{A}a_{A}$
$\mu_{1}m_{A}g - \mu_{2}(m_{A} + m_{B})g = m_{B}a_{B}$
解得$a_{A} = 2m/s^{2}$,$a_{B} = 1m/s^{2}$
由运动学规律,对B:$x_{1} = \frac{1}{2}a_{B}t_{1}^{2}$
对A:$v_{1} = v_{0} - a_{A}t_{1}$
解得$v_{1} = 4m/s$,$v_{2} = a_{B}t_{1} = 1m/s$。
(2)木板B与物块C相碰,设碰后B、C的速度分别为$v_{3}$、$v_{4}$
由动量守恒定律和能量守恒定律可得$m_{B}v_{2} = m_{B}v_{3} + m_{C}v_{4}$
$\frac{1}{2}m_{B}v_{2}^{2} = \frac{1}{2}m_{B}v_{3}^{2} + \frac{1}{2}m_{C}v_{4}^{2}$
解得$v_{3} = 0$,$v_{4} = 1m/s$
碰后C做匀减速运动,设加速度大小为$a_{C}$,经历时间为$t_{3}$,位移为$x_{2}$,
则$\mu_{2}m_{C}g = m_{C}a_{C}$
解得$a_{C} = 1m/s^{2}$
第二次碰撞前C静止,则$v_{4} = a_{C}t_{3}$
解得时间为$t_{3} = 1s$
此时运动距离为$x_{2} = \frac{1}{2}a_{C}t_{3}^{2} = 0.5m$
由$x = \frac{1}{2}a_{B}t_{3}^{2}$知B在$1s$内恰好移动$0.5m$,B追上C,二者加速度大小相同,B加速,C减速,故所需时间为$1s$,即从第一次碰撞到第二次碰撞经历时间为$1s$。
(3)第二次碰撞后,设A的速度为$v_{5}$,由运动学规律可得$v_{5} = v_{1} - a_{A}t_{3}$
设木板与物块A达到共速时,速度为$v_{6}$,时间为$t_{4}$,则$v_{6} = v_{5} - a_{A}t_{4}$,$v_{6} = a_{B}t_{4}$
设木板共速之前的位移为$x_{3}$,共速之后的位移为$x_{4}$,
则$x_{3} = \frac{1}{2}a_{B}t_{4}^{2}$,$v_{6}^{2} = 2a_{B}x_{4}$,$x = x_{2} - x_{3} - x_{4}$,解得$x = \frac{1}{18}m$。
查看更多完整答案,请扫码查看


