《2026年学易优高考二轮总复习物理》

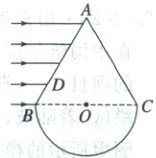
1. (2025·河南省模拟)如图所示，“水滴形”透明体其纵截面由等边三角形和半圆形组成，三角形的三个顶点分别为$ A、B、C $，边长为$ L $。一束平行于$ BC $边的光线入射到$ AB $边上，只有$ BD $区域的光线能够射入半球体，$ BD $长度等于$\frac{L}{4}$，不考虑反射，$\sqrt{13}=3.6$。光在真空中的传播速度为$ c $。求：
(1)该透明介质的折射率；
(2)折射光线在半球体中传播的最长时间。

答案：
1.答案:
(1)1.8
(2)$\frac{7L}{4c}$
解析:
(1)从D点入射的光线,恰好从C点射入半球，光路如图所示。设折射角为$\theta$，由正弦定理有$\frac{L}{\sin(30^{\circ}-\theta)}=\frac{L}{\sin(90^{\circ}+\theta)}$
又$n=\frac{\sin30^{\circ}}{\sin\theta}$，得$n=\frac{\sqrt{13}}{2}=1.8$。

(2)依题意，可知光线在半球体中传播的最长路程为$x = L\cos(30^{\circ}-\theta)$
由$x = vt$，$n=\frac{c}{v}$，联立求得$t=\frac{7L}{4c}$。

2. 清代乾隆的《冰嬉赋》用“躣躣”（可理解为低身斜体）二字揭示了滑冰的动作要领。$ 500 \, m $短道速滑世界纪录由我国运动员武大靖创造并保持。在其创造纪录的比赛中。
(1)武大靖从静止出发，先沿直道加速滑行，前$ 8 \, m $用时$ 2 \, s $。该过程可视为匀加速直线运动，求此过程加速度大小；
(2)武大靖途中某次过弯时的运动可视为半径为$ 10 \, m $的匀速圆周运动，速度大小为$ 14 \, m/s $。已知武大靖的质量为$ 73 \, kg $，求此次过弯时所需的向心力大小；
(3)武大靖通过侧身来调整身体与水平冰面的夹角，使场地对其作用力指向身体重心而实现平稳过弯，如图所示。求武大靖在(2)问中过弯时身体与水平面的夹角$ \theta $的大小。（不计空气阻力，重力加速度大小取$ 10 \, m/s^2 $，$\tan 22° = 0.40$、$\tan 27° = 0.51$、$\tan 32° = 0.62$、$\tan 37° = 0.75$）

答案：
2.答案:
(1)4m/s²
(2)1430.8N
(3)27°
解析:
(1)设武大靖运动过程的加速度大小为$a$，根据$x=\frac{1}{2}at^{2}$解得$a=\frac{2x}{t^{2}}=\frac{2×8}{2^{2}}m/s^{2}=4m/s^{2}$。
(2)根据$F_{n}=m\frac{v^{2}}{r}$
解得过弯时所需的向心力大小为$F_{n}=73×\frac{14^{2}}{10}N = 1430.8N$。
(3)设场地对武大靖的作用力大小为$F$，受力如图所示

根据牛顿第二定律可得$F_{n}=\frac{mg}{\tan\theta}$
解得$\tan\theta=\frac{mg}{F_{n}}=\frac{73×10}{1430.8}\approx0.51$
可得$\theta = 27^{\circ}$。