12. 在$\triangle ABC$中,$AB=3\sqrt{6}$,$AC=6$,$\angle B=45^{\circ}$,则$BC=$
3$\sqrt{3}$+3或3$\sqrt{3}$−3
.
答案:
12.3$\sqrt{3}$+3或3$\sqrt{3}$−3
13. 定义一种运算:$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$,$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$.
例如:当$\alpha=45^{\circ}$,$\beta=30^{\circ}$时,$\sin(45^{\circ}+30^{\circ})=\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$,则$\sin15^{\circ}$的值为
例如:当$\alpha=45^{\circ}$,$\beta=30^{\circ}$时,$\sin(45^{\circ}+30^{\circ})=\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$,则$\sin15^{\circ}$的值为
$\frac{\sqrt{6}}{4}$−$\frac{\sqrt{2}}{4}$
.
答案:
13.$\frac{\sqrt{6}}{4}$−$\frac{\sqrt{2}}{4}$
14. 图(1)是光伏发电场景,其示意图如图(2),$EF$为吸热塔,在地平线$EG$上的点$B$,$B'$处各安装定日镜[介绍见图(3)].绕各中心点($A$,$A'$)旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点$F$处.已知$AB=A'B'=1\ m$,$EB=8\ m$,$EB'=8\sqrt{3}\ m$,在点$A$观测点$F$的仰角为$45^{\circ}$.点$F$的高度$EF$为
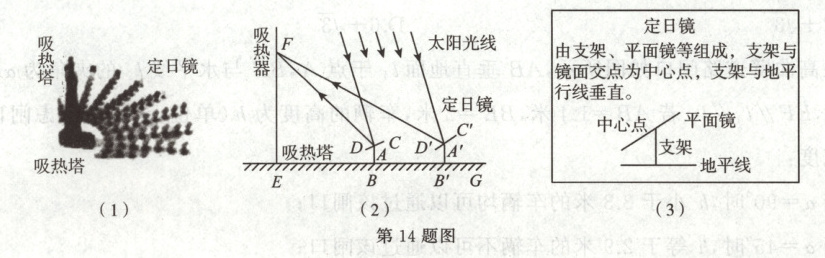
9
$ m$.
答案:
14.9
15. (16 分)计算:(1)$2\sin30^{\circ}+3\cos60^{\circ}-4\tan45^{\circ}$;(2)$\frac{\cos^{2}30^{\circ}}{1+\sin30^{\circ}}+\tan^{2}60^{\circ}$.
答案:
15.解:
(1)原式=2×$\frac{1}{2}$+3×$\frac{1}{2}$−4×1=1+$\frac{3}{2}$−4=−$\frac{3}{2}$.
(2)原式=$\frac{(-\frac{\sqrt{3}}{2})^2}{1+\frac{1}{2}}$+($\sqrt{3}$)²=$\frac{\frac{3}{4}}{\frac{3}{2}}$+3=$\frac{7}{2}$.
(1)原式=2×$\frac{1}{2}$+3×$\frac{1}{2}$−4×1=1+$\frac{3}{2}$−4=−$\frac{3}{2}$.
(2)原式=$\frac{(-\frac{\sqrt{3}}{2})^2}{1+\frac{1}{2}}$+($\sqrt{3}$)²=$\frac{\frac{3}{4}}{\frac{3}{2}}$+3=$\frac{7}{2}$.
16. (14 分)如图,在$\triangle ABC$中,$\angle ACB=45^{\circ}$,$\tan B=\frac{2}{3}$,$BC=10$.
(1)求$AB$的长;(2)如果$CD$为边$AB$上的中线,求$\angle DCB$的正切值.
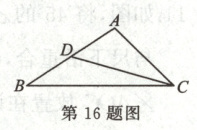
(1)求$AB$的长;(2)如果$CD$为边$AB$上的中线,求$\angle DCB$的正切值.

答案:
16.解:
(1)过A作AE⊥BC于E,作DF⊥BC于F.
因为∠BCA=45°,
所以在Rt△AEC中,AE =EC.
因为tanB=$\frac{3}{2}$,
所以在Rt△BEA中,$\frac{AE}{BE}$=$\frac{2}{3}$.
设BE=3x,AE=2x,
所以BC=BE+EC=BE+AE=10,
所以x=2,
所以BE=6,EA=EC=4.
由勾股定理得AE²+BE²=AB²,
即AB²=36+16=52,
所以AB=$\sqrt{52}$=2$\sqrt{13}$.

(2)由
(1)知AB=2$\sqrt{13}$,
又因为D为AB的中点,
所以BD=AD=$\sqrt{13}$.
因为DF⊥BC,AE⊥BC,
所以DF//AE.
因为BD=AD,
所以BF=FE=$\frac{1}{2}$BE=3,
所以DF=$\frac{1}{2}$AE=2,
所以FC=FE+EC=3+4=7,
所以tan∠DCB=$\frac{2}{7}$.
16.解:
(1)过A作AE⊥BC于E,作DF⊥BC于F.
因为∠BCA=45°,
所以在Rt△AEC中,AE =EC.
因为tanB=$\frac{3}{2}$,
所以在Rt△BEA中,$\frac{AE}{BE}$=$\frac{2}{3}$.
设BE=3x,AE=2x,
所以BC=BE+EC=BE+AE=10,
所以x=2,
所以BE=6,EA=EC=4.
由勾股定理得AE²+BE²=AB²,
即AB²=36+16=52,
所以AB=$\sqrt{52}$=2$\sqrt{13}$.

(2)由
(1)知AB=2$\sqrt{13}$,
又因为D为AB的中点,
所以BD=AD=$\sqrt{13}$.
因为DF⊥BC,AE⊥BC,
所以DF//AE.
因为BD=AD,
所以BF=FE=$\frac{1}{2}$BE=3,
所以DF=$\frac{1}{2}$AE=2,
所以FC=FE+EC=3+4=7,
所以tan∠DCB=$\frac{2}{7}$.
查看更多完整答案,请扫码查看


