《2025年行知天下九年级数学上册青岛版》

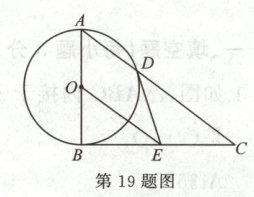
19. (16 分)如图,在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,以$AB$的中点$O$为圆心、$OA$为半径的圆交$AC$于点$D$,$E$是$BC$的中点,连接$DE$,$OE$.
(1) 判断$DE$与$\odot O$的位置关系,并说明理由;
(2) 求证:$BC^{2} = CD · 2OE$;
(3) 若$AB:AC = 3:5$,$BE = 6$,求$OE$的长.

答案：
19.
(1)解:DE与⊙O相切.
理由:连接OD,BD.
因为AB为圆O的直径，
所以∠ADB=90°.
在Rt△BDC中,E为斜边BC的中点，
所以CE=DE=BE=$\frac{1}{2}$BC,
所以∠C=∠CDE.
因为OA=OD,
所以∠A=∠ADO.
因为∠ABC=90°,即∠C+∠A=90°,
所以∠ADO+∠CDE=90°,即∠ODE=90°,所以DE⊥OD.
因为OD为圆的半径，
所以DE为⊙O的切线.
(2)证明:因为E是BC的中点,O点是AB的中点，
所以OE是△ABC的中位线，
所以AC=2OE.
因为∠C=∠C,∠ABC=∠BDC,
所以△ABC∽△BDC，
所以$\frac{BC}{CD}$=$\frac{AC}{BC}$,即BC²=AC·CD,
所以BC²=2CD·OE.
(3)解:因为AB:AC=3:5，
所以sin∠BAC =$\frac{BC}{AC}$=$\frac{4}{5}$.
又因为BE=6，E是BC的中点，即BC =12，
所以AC=15.
又因为AC=2OE，
所以OE=$\frac{1}{2}$AC=$\frac{15}{2}$.