13.如图,在$\bigtriangleup ABC$中,$\angle BAC = 60^{\circ}$,$\angle ABC = 90^{\circ}$,直线$l_{1} // l_{2} // l_{3}$,$l_{1}$与$l_{2}$之间距离是$1$,$l_{2}$与$l_{3}$之间距离是$2$,且$l_{1}$,$l_{2}$,$l_{3}$分别经过点$A$,$B$,$C$,则边$AC$的长为
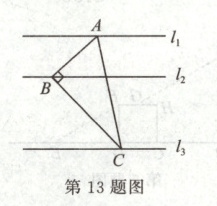
$\frac{2}{3}\sqrt{21}$
.
答案:
13.$\frac{2}{3}\sqrt{21}$
14.如图,$\bigtriangleup ABC$是边长为$6\ cm$等边三角形,动点$P$,$Q$同时从$A$,$B$出发,分别沿$AB$,$BC$方向匀速运动,其中点$P$运动的速度是$1\ cm/s$,点$Q$运动的速度是$2\ cm/s$.当点$Q$到达点$C$时,$P$,$Q$两点停止运动.在运动过程中作$QR // BA$,交$AC$于点$R$,连接$PR$,设运动的时间为$t(s)$,当$t =$
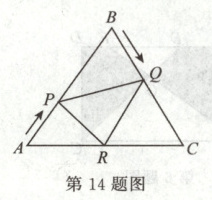
1.2
$s$时,$\bigtriangleup APR \backsim \bigtriangleup PRQ$.
答案:
14.1.2
15.(10分)如图,在$\bigtriangleup ABC$中,$CD$是边$AB$上的高,且$\frac{AD}{CD} = \frac{CD}{BD}$.
(1)求证:$\bigtriangleup ACD \backsim \bigtriangleup CBD$;
(2)求$\angle ACB$的大小.
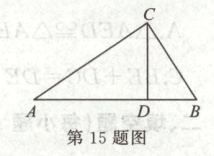
(1)求证:$\bigtriangleup ACD \backsim \bigtriangleup CBD$;
(2)求$\angle ACB$的大小.

答案:
15.
(1)证明:因为CD是边AB上的高,
所以∠ADC = ∠CDB = 90°.
因为$\frac{AD}{CD}=\frac{CD}{BD}$,
所以△ACD∽△CBD.
(2)解:因为△ACD∽△CBD,
所以∠A = ∠BCD.
在△ACD中,因为∠ADC = 90°,
所以∠A + ∠ACD = 90°,
所以∠BCD + ∠ACD = 90°,
即∠ACB = 90°.
(1)证明:因为CD是边AB上的高,
所以∠ADC = ∠CDB = 90°.
因为$\frac{AD}{CD}=\frac{CD}{BD}$,
所以△ACD∽△CBD.
(2)解:因为△ACD∽△CBD,
所以∠A = ∠BCD.
在△ACD中,因为∠ADC = 90°,
所以∠A + ∠ACD = 90°,
所以∠BCD + ∠ACD = 90°,
即∠ACB = 90°.
16.(10分)如图,$\angle ABD = \angle BCD = 90^{\circ}$,$DB$平分$\angle ADC$,过点$B$作$BM // CD$交$AD$于$M$.连接$CM$交$DB$于$N$.
(1)求证:$BD^{2} = AD · CD$;
(2)若$CD = 6$,$AD = 8$,求$MN$的长.
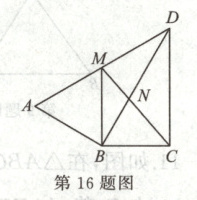
(1)求证:$BD^{2} = AD · CD$;
(2)若$CD = 6$,$AD = 8$,求$MN$的长.

答案:
16.
(1)证明:因为DB平分∠ADC,
所以∠ADB = ∠CDB,且∠ABD = ∠BCD = 90°,
所以△ABD∽△BCD,
所以$\frac{AD}{BD}=\frac{BD}{CD}$,
所以BD² = AD·CD.
(2)解:因为BM//CD,
所以∠MBD = ∠BDC,
所以∠ADB = ∠MBD,且∠ABD = 90°,
所以BM = MD,∠MAB = ∠MBA,
所以BM = MD = AM = 4.
因为BD² = AD·CD,且CD = 6,AD = 8,
所以BD² = 48,
所以BC² = BD² - CD² = 12,
所以MC² = MB² + BC² = 28,
所以MC = 2$\sqrt{7}$.
因为BM//CD,
所以△MNB∽△CND,
所以$\frac{BM}{CD}=\frac{MN}{CN}=\frac{2}{3}$,且MC = 2$\sqrt{7}$,
所以MN = $\frac{4}{5}\sqrt{7}$.
(1)证明:因为DB平分∠ADC,
所以∠ADB = ∠CDB,且∠ABD = ∠BCD = 90°,
所以△ABD∽△BCD,
所以$\frac{AD}{BD}=\frac{BD}{CD}$,
所以BD² = AD·CD.
(2)解:因为BM//CD,
所以∠MBD = ∠BDC,
所以∠ADB = ∠MBD,且∠ABD = 90°,
所以BM = MD,∠MAB = ∠MBA,
所以BM = MD = AM = 4.
因为BD² = AD·CD,且CD = 6,AD = 8,
所以BD² = 48,
所以BC² = BD² - CD² = 12,
所以MC² = MB² + BC² = 28,
所以MC = 2$\sqrt{7}$.
因为BM//CD,
所以△MNB∽△CND,
所以$\frac{BM}{CD}=\frac{MN}{CN}=\frac{2}{3}$,且MC = 2$\sqrt{7}$,
所以MN = $\frac{4}{5}\sqrt{7}$.
查看更多完整答案,请扫码查看


