《2025年同步测控优化设计六年级数学上册北师大版》

1. 统计知识在生活中应用广泛，(扇形)统计图能清楚地反映各部分与整体之间的关系；(折线)统计图既可以表示数量的多少，又能清楚地反映数量增减变化趋势；从(条形)统计图能很快地看出数量的多少和数量之间的差异。

答案： 扇形 折线 条形

2. 要统计某一地区一周气温变化的情况，设计(折线)统计图最合适。

答案： 折线

3. 用统计图绘制我国五大名山主峰的海拔情况，绘制(条形)统计图最合适。

答案： 条形

4. 六(1)班进行体育测试，80分及80分以上的人数占94%(优秀率)，60~79分的人数占4%，不及格的人数占2%。

这些数据选用(扇形)统计图表示比较合适。

答案： 50 扇形

5. 小丽最喜欢吃水果了，右面是她根据去年妈妈买的三种水果质量制成的扇形统计图。

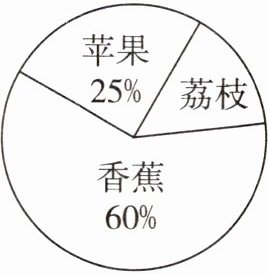
(1)去年妈妈所买的荔枝质量占水果总质量的(15)%。如果荔枝买了48kg，那么苹果买了(80)kg，香蕉买了(192)kg。
(2)去年妈妈所买的荔枝质量是苹果质量的$\frac{(3)}{(5)}$，是香蕉质量的$\frac{(1)}{(4)}$。

答案：
(1)15 80 192
(2)$\frac{3}{5}$ $\frac{1}{4}$

二、我是小法官。(正确的画“√”，错误的画“×”)
1. 要比较两组同学的体重情况，只能比较他们的平均体重。(×)
2. 折线统计图只能反映事物(数量)变化的情况。(×)
3. 医院对病人每4时量一次体温，要反映病人24时内的体温数据，可以选择条形、折线、扇形统计图中的任何一种。(×)
4. 要表示出六年级各班的具体人数，选用条形统计图最合适。(√)
5. 空气是由多种气体组成的，用扇形统计图能表示空气中各种成分的含量情况。(√)

答案： 1. × 2. × 3. × 4. √ 5. √

三、看统计图回答问题。
A小学举行硬笔书法比赛，40幅获奖作品的获奖等级如下图所示。
A小学硬笔书法比赛获奖作品等级情况统计图

1. 获奖作品占参赛作品的25%，参赛作品共有多少幅？
2. 获得二等奖的作品比获得一等奖的作品多多少幅？

答案： 1. 已知获奖作品数为$40$幅，且获奖作品占参赛作品的$25\%$，则参赛作品总数为：
$40÷25\% = 40÷0.25 = 160$（幅）
答：参赛作品共有$160$幅。
2. 获得一等奖的作品数量为：
$40×15\% = 40×0.15 = 6$（幅）
获得二等奖的作品数量为：
$40×35\% = 40×0.35 = 14$（幅）
获得二等奖的作品比获得一等奖的作品多的数量为：
$14 - 6 = 8$（幅）
答：获得二等奖的作品比获得一等奖的作品多$8$幅。