1. 我国南北朝时期著名的数学家(
祖冲之
)得到了π的两个分数形式的近似值。
答案:
祖冲之
2. 一个钟表的分针长5cm,经过1时,分针针尖走过的路程是(
31.4 cm
),经过30分,分针针尖走过的路程是(15.7 cm
)。
答案:
2. 31.4 cm 15.7 cm
3. 若量角器的周长是20.56cm,则它的半径长(
4
)cm,圆弧长(12.56
)cm。
答案:
3. 4 12.56
1. 圆的周长是半径的(
A.π
B.3.14
C.4
D.2π
D
)倍。A.π
B.3.14
C.4
D.2π
答案:
1. D
2. 两个圆的周长不相等,是因为(
A.圆心的位置不同
B.半径不相等
C.圆周率不相等
D.使用的圆规不同
B
)。A.圆心的位置不同
B.半径不相等
C.圆周率不相等
D.使用的圆规不同
答案:
2. B
3. 若两圆的直径相差4cm,则两圆的周长相差(
A.4cm
B.2πcm
C.4πcm
D.6.28cm
C
)。A.4cm
B.2πcm
C.4πcm
D.6.28cm
答案:
3. C
4. 一台拖拉机,后轮直径是前轮直径的2倍,后轮滚动4圈,前轮滚动(
A.4
B.8
C.16
D.32
B
)圈。A.4
B.8
C.16
D.32
答案:
4. B
1. 王叔叔骑自行车从家到书店,车轮转动了500周。若车轮半径为28cm,则王叔叔家到书店有多少米?
答案:
1. 879.2 m
2. 某地有一棵千年古树,树的直径达12.4m,至少需要多少名身高为1.3m的小学生伸开双臂才能围住这棵大树?


答案:
2. $3.14×12.4÷1.3\approx30$(名)
四、动脑筋。
如图,小强与小军在环形跑道上赛跑,小强跑内道,小军跑外道,起点和终点相同,这样比赛公平吗?如果你认为不公平,那么该怎样解决?
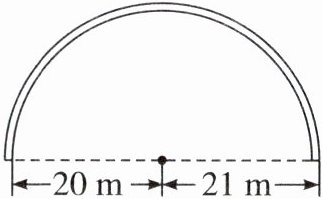
如图,小强与小军在环形跑道上赛跑,小强跑内道,小军跑外道,起点和终点相同,这样比赛公平吗?如果你认为不公平,那么该怎样解决?

答案:
(提示:圆的半径不同,周长就不同,周长的一半也不相同,所以两个人跑的路程不同,比赛是不公平的。通过调整起点或终点,把两个人跑的路程设置一样就可以了。)小强跑的路程:$3.14×20×2÷2=62.8(m)$小军跑的路程:$3.14×21×2÷2=65.94(m)$$65.94 - 62.8=3.14(m)$答:这样的比赛不公平。我认为可以这样解决:小军的起跑点定在小强的起跑点前3.14 m处,终点相同,这样两个人跑的路程就相同了,比赛就公平了。
查看更多完整答案,请扫码查看


