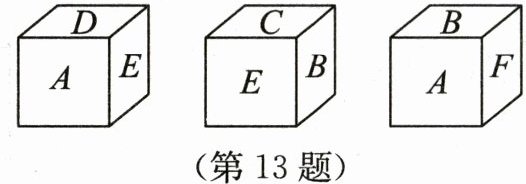
13. 一个小立方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.已知A、B、C、D、E、F分别代表数字-2、-1、0、1、2、3,则这三个方向的下底面所标字母代表的数字的和为
4
.
答案:
4
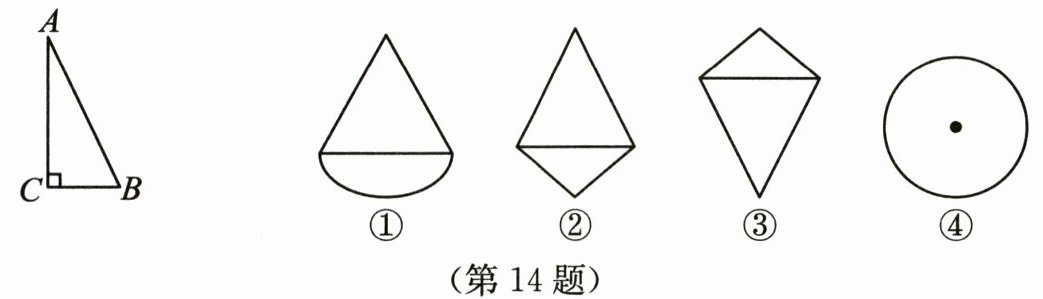
14. 如图,将Rt△ABC绕AB旋转一周所得的几何体的主视图是
①
(填序号).
答案:
①
15. 用6根长度相等的火柴棒搭等边三角形,最多可搭成
4
个.
答案:
4
16. 某玩具厂在生产配件时需要分别从棱长为2a的正方体木块中挖去一个棱长为a的小正方体木块,得到甲、乙、丙三种型号的玩具配件(如图).将甲、乙、丙这三种配件的表面积分别记为S甲、S乙和S丙,则S甲、S乙和S丙大小关系为

$S_{甲}>S_{乙}>S_{丙}$
(用“>”连接,几何体的表面积是指几何体所有表面的面积之和).
答案:
$S_{甲}>S_{乙}>S_{丙}$
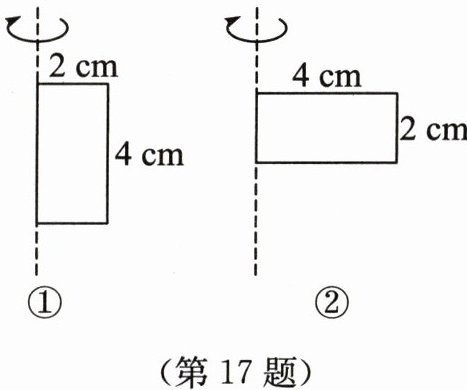
17. (10分)如图,将长和宽分别为4cm和2cm的长方形分别绕图①和图②中的虚线轴旋转一周得到甲、乙两个几何体.这两个几何体的体积相等吗?如果不相等,那么哪个几何体的体积较大?(结果保留π)

答案:
解题过程如下:
不相等。
绕图①中的虚线轴旋转一周得到的甲几何体体积:
$V_{甲} = \pi × 2^{2} × 4 = 16\pi (cm^{3})$。
绕图②中的虚线轴旋转一周得到的乙几何体体积:
$V_{乙} = \pi × 4^{2} × 2 = 32\pi (cm^{3})$。
因为 $16\pi \lt 32\pi$,
故,乙几何体的体积较大。
不相等。
绕图①中的虚线轴旋转一周得到的甲几何体体积:
$V_{甲} = \pi × 2^{2} × 4 = 16\pi (cm^{3})$。
绕图②中的虚线轴旋转一周得到的乙几何体体积:
$V_{乙} = \pi × 4^{2} × 2 = 32\pi (cm^{3})$。
因为 $16\pi \lt 32\pi$,
故,乙几何体的体积较大。
查看更多完整答案,请扫码查看


