《2025年新课程学习指导海南出版社五年级数学上册人教版》

(1)剪一剪：动手剪两个完全一样的梯形。
(2)拼一拼：用手中的梯形拼一拼,能拼成已学过的什么图形？
(3)想一想：拼成的图形的底和高与原梯形的底和高有什么关系？
[发现]梯形的面积= 等底等高平行四边形的面积÷2

答案： （1）剪两个完全一样的梯形。
(2)能拼成平行四边形。
(3)两个完全一样的梯形可以拼成一个平行四边形，拼成的平行四边形的底等于梯形的上底与下底的和，高等于梯形的高。

(1)我们在推导梯形的面积公式时,用到了“转化”的方法,把两个一模一样的梯形拼成一个平行四边形。

梯形的(上底与下底的和)相当于平行四边形的底；梯形的高相当于平行四边形的(高)。所以这个梯形面积是所拼成平行四边形面积的(一半)。梯形的面积公式为($S=(a+b)h÷2$)。

答案： 上底与下底的和  高  一半
$S=(a+b)h÷2$

(2)一个梯形的上底是8m,下底是12m,高是5m,这个梯形的面积是(50)m²。

答案： 50

(3)一个梯形的面积是$42cm^2,$上底是5cm,高是6cm,下底是(9)cm。

答案： 9

(4)求出表格中梯形的面积。

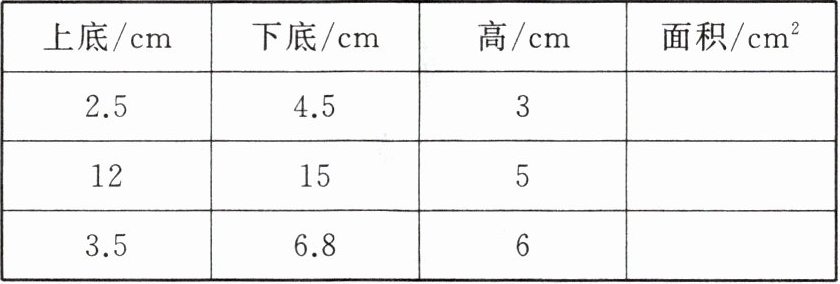
10.5 67.5 30.9

答案： 10.5 67.5 30.9

(1)一个梯形的下底是12cm,上底与高相等,都是10cm,它的面积是(A)$cm^2。$
A.110
B.220
C.120

答案： A

(2)梯形的上底减少2cm,下底增加2cm,高不变,则梯形的面积(B)。
A.增加$4cm^2$
B.不变
C.减少$4cm^2$

答案： B