第33页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
8. 在“探究杠杆的平衡条件”实验中。
(1)实验前,将杠杆置于支架上,当杠杆静止时,发现左端下沉,如图①所示,此时,应把杠杆的平衡螺母向______(填“左”或“右”)调节,直至杠杆在______(填“任意”或“水平”)位置平衡。
(2)调节平衡后,在杠杆上A点处挂两个钩码,如图②所示,则在B点处应挂______个钩码,才能使杠杆在原位置平衡。在A、B两点各增加1个钩码,则杠杆______(填“能”或“不能”)保持平衡。(所挂钩码均相同)
(3)为了使实验结论具有______(填“普遍性”或“偶然性”),应改变钩码个数及悬挂位置,多次进行实验。
(4)实验时,不再调节平衡螺母,使杠杆的重心位置保持在O点不变,将支点换到O'点,如图③所示,发现A点处只挂1个钩码,杠杆仍然保持平衡。若每个钩码重为0.5 N,则杠杆重力为______N。由此可知,将杠杆支点位置设在______(填“O”或“O'”)点进行实验,能避免杠杆自身重力影响实验结论“动力×动力臂= 阻力×阻力臂”的得出。

(1)实验前,将杠杆置于支架上,当杠杆静止时,发现左端下沉,如图①所示,此时,应把杠杆的平衡螺母向______(填“左”或“右”)调节,直至杠杆在______(填“任意”或“水平”)位置平衡。
(2)调节平衡后,在杠杆上A点处挂两个钩码,如图②所示,则在B点处应挂______个钩码,才能使杠杆在原位置平衡。在A、B两点各增加1个钩码,则杠杆______(填“能”或“不能”)保持平衡。(所挂钩码均相同)
(3)为了使实验结论具有______(填“普遍性”或“偶然性”),应改变钩码个数及悬挂位置,多次进行实验。
(4)实验时,不再调节平衡螺母,使杠杆的重心位置保持在O点不变,将支点换到O'点,如图③所示,发现A点处只挂1个钩码,杠杆仍然保持平衡。若每个钩码重为0.5 N,则杠杆重力为______N。由此可知,将杠杆支点位置设在______(填“O”或“O'”)点进行实验,能避免杠杆自身重力影响实验结论“动力×动力臂= 阻力×阻力臂”的得出。
答案:
(1)右;水平
(2)$4$;不能
(3)普遍性
(4)$1$;$O$
(1)右;水平
(2)$4$;不能
(3)普遍性
(4)$1$;$O$
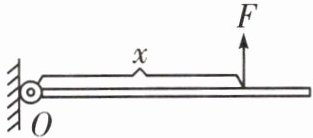
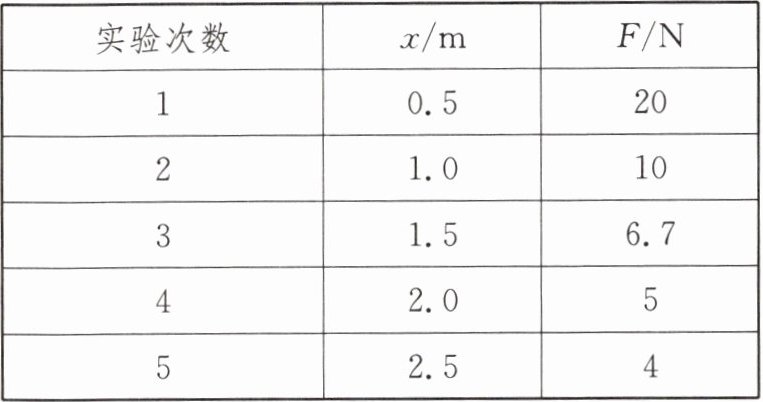
9. 如图所示,长3.0 m、重10 N且密度不均匀的金属杆,绕O点在竖直平面内自由转动。现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离x及F的大小;再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如表所示。
| 实验次数 | x/m | F/N |
| 1 | 0.5 | 20 |
| 2 | 1.0 | 10 |
| 3 | 1.5 | 6.7 |
| 4 | 2.0 | 5 |
| 5 | 2.5 | 4 |
(1)由表中数据可得F与x之间的关系式:______。
(2)计算O点到金属杆重心的距离。
(3)若弹簧测力计量程为0~25 N,计算弹簧测力计的移动范围。

| 实验次数 | x/m | F/N |
| 1 | 0.5 | 20 |
| 2 | 1.0 | 10 |
| 3 | 1.5 | 6.7 |
| 4 | 2.0 | 5 |
| 5 | 2.5 | 4 |

(1)由表中数据可得F与x之间的关系式:______。
(2)计算O点到金属杆重心的距离。
(3)若弹簧测力计量程为0~25 N,计算弹簧测力计的移动范围。
答案:
(1) $ F = \frac{10}{x} $ (N)
(2) 解:设O点到金属杆重心的距离为$ l $,金属杆重$ G = 10\ N $。根据杠杆平衡条件$ Fx = Gl $,取实验数据$ x = 1.0\ m $,$ F = 10\ N $,得$ 10\ N × 1.0\ m = 10\ N × l $,解得$ l = 1.0\ m $
(3) 解:由$ F = \frac{10}{x} $,当$ F = 25\ N $时,$ x = \frac{10}{25} = 0.4\ m $;金属杆长3.0 m,$ x $最大为3.0 m。故移动范围为$ 0.4\ m \leq x \leq 3.0\ m $
(1) $ F = \frac{10}{x} $ (N)
(2) 解:设O点到金属杆重心的距离为$ l $,金属杆重$ G = 10\ N $。根据杠杆平衡条件$ Fx = Gl $,取实验数据$ x = 1.0\ m $,$ F = 10\ N $,得$ 10\ N × 1.0\ m = 10\ N × l $,解得$ l = 1.0\ m $
(3) 解:由$ F = \frac{10}{x} $,当$ F = 25\ N $时,$ x = \frac{10}{25} = 0.4\ m $;金属杆长3.0 m,$ x $最大为3.0 m。故移动范围为$ 0.4\ m \leq x \leq 3.0\ m $
查看更多完整答案,请扫码查看


