11. 如图是一块三角形木板的残余部分,量得$\angle A= 100^{\circ}$,$\angle B= 40^{\circ}$,则这块三角形木板另外一个角$\angle C$的度数为(
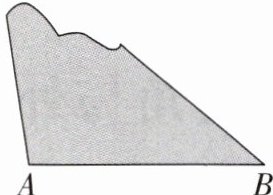
A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
B
)
A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
答案:
B
12. 具备下列条件的$\triangle ABC$中,不是直角三角形的是(
A.$\angle A= \angle B= 3\angle C$
B.$\angle A-\angle B= \angle C$
C.$\angle A+\angle B= \angle C$
D.$\angle A:\angle B:\angle C= 1:2:3$
A
)A.$\angle A= \angle B= 3\angle C$
B.$\angle A-\angle B= \angle C$
C.$\angle A+\angle B= \angle C$
D.$\angle A:\angle B:\angle C= 1:2:3$
答案:
A
13. 如图,$CE是\triangle ABC的外角\angle ACD$的平分线.若$\angle B= 40^{\circ}$,$\angle ACE= 65^{\circ}$,则$\angle A$的度数为(
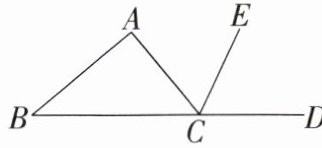
A.$95^{\circ}$
B.$90^{\circ}$
C.$85^{\circ}$
D.$80^{\circ}$
B
)
A.$95^{\circ}$
B.$90^{\circ}$
C.$85^{\circ}$
D.$80^{\circ}$
答案:
B
14. 如图,$\triangle ABC的两个外角的平分线相交于点O$.若$\angle A= 80^{\circ}$,则$\angle O$的度数为(
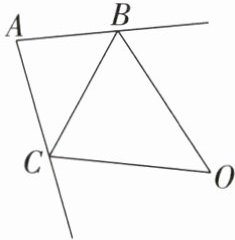
A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$80^{\circ}$
B
)
A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$80^{\circ}$
答案:
B
15. 如图,把$\triangle ABC纸片沿DE$折叠,则( )
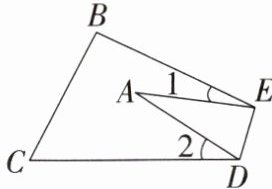
A.$\angle A= \angle 1+\angle 2$
B.$2\angle A= \angle 1+\angle 2$
C.$3\angle A= 2\angle 1+\angle 2$
D.$3\angle A= 2(\angle 1+\angle 2)$

A.$\angle A= \angle 1+\angle 2$
B.$2\angle A= \angle 1+\angle 2$
C.$3\angle A= 2\angle 1+\angle 2$
D.$3\angle A= 2(\angle 1+\angle 2)$
答案:
解析:选B.如图,分别延长BE,CD,交于点F,连接AF.

由题可知∠EAD=∠EFD.
因为∠1=∠EAF+∠EFA,∠2=∠DAF +∠AFD,
所以∠1+∠2=∠EAF+∠EFA+∠DAF +∠AFD.
所以∠1+∠2=∠EAD+∠EFD.
所以∠1+∠2=2∠EAD.
故选B.
解析:选B.如图,分别延长BE,CD,交于点F,连接AF.

由题可知∠EAD=∠EFD.
因为∠1=∠EAF+∠EFA,∠2=∠DAF +∠AFD,
所以∠1+∠2=∠EAF+∠EFA+∠DAF +∠AFD.
所以∠1+∠2=∠EAD+∠EFD.
所以∠1+∠2=2∠EAD.
故选B.
16. 如图所示的几何图形,$\angle A+\angle B+\angle C+\angle D+\angle E$的度数为(
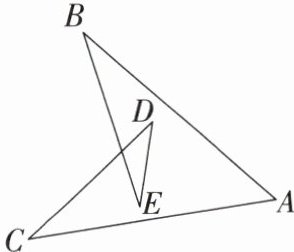
A.$360^{\circ}$
B.$270^{\circ}$
C.$240^{\circ}$
D.$180^{\circ}$
D
)
A.$360^{\circ}$
B.$270^{\circ}$
C.$240^{\circ}$
D.$180^{\circ}$
答案:
D
17. 如图是$A$,$B$,$C$三岛的平面图,$C岛在A岛的北偏东40^{\circ}$方向,$B岛在A岛的北偏东80^{\circ}$方向,$C岛在B岛的北偏西50^{\circ}$方向.从$C岛看A$,$B岛的视角\angle ACB$为多少度?
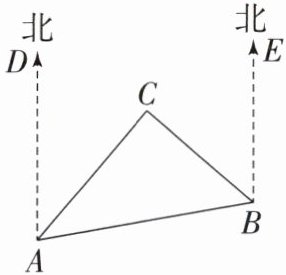

答案:
解:由题意,得∠DAB=80°.
因为DA//EB,
所以∠EBA=180°−∠DAB=100°.
又∠EBC=50°,
所以∠ABC=∠EBA−∠EBC=50°.
因为∠DAB=80°,∠DAC=40°,
所以∠CAB=40°,
所以∠ACB=180°−∠CAB−∠ABC =90°.
因为DA//EB,
所以∠EBA=180°−∠DAB=100°.
又∠EBC=50°,
所以∠ABC=∠EBA−∠EBC=50°.
因为∠DAB=80°,∠DAC=40°,
所以∠CAB=40°,
所以∠ACB=180°−∠CAB−∠ABC =90°.
18. 如图,$\angle A= 70^{\circ}$,$P是\triangle ABC$内一点,$BP平分\angle ABC$,$CP平分\angle ACB$,则$\angle BPC$的度数为(
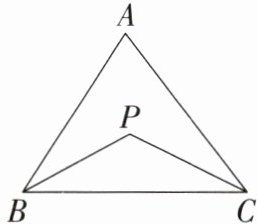
A.$105^{\circ}$
B.$115^{\circ}$
C.$125^{\circ}$
D.$135^{\circ}$
C
)
A.$105^{\circ}$
B.$115^{\circ}$
C.$125^{\circ}$
D.$135^{\circ}$
答案:
C
19. 将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则$\angle 1$的度数是(
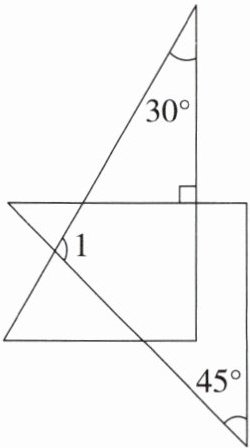
A.$95^{\circ}$
B.$100^{\circ}$
C.$105^{\circ}$
D.$110^{\circ}$
C
)
A.$95^{\circ}$
B.$100^{\circ}$
C.$105^{\circ}$
D.$110^{\circ}$
答案:
C
查看更多完整答案,请扫码查看


