7. 在直角三角形中,如果一个锐角等于 $30^{\circ}$,那么它所对的直角边等于斜边的
一半
.
答案:
一半
8. 如图,一水库迎水坡 $AB$ 的长度为 $20$ m,斜坡与水平面的夹角 $\alpha$ 为 $30^{\circ}$,则迎水坡的高度是
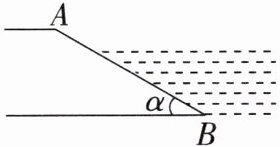
10
m.
答案:
10
9. 如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$\angle B = 30^{\circ}$,$D$ 为线段 $AB$ 的中点,则 $\angle ADC$ 的度数为
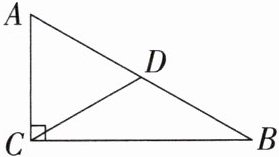
60°
.
答案:
解析:因为∠ACB=90°,∠B=30°,所以∠A=60°,AC= $\frac{1}{2}$AB.因为 D 为线段 AB 的中点,所以 AD= $\frac{1}{2}$AB,所以 AD=AC,所以△ACD 是等边三角形,所以∠ADC=60°.答案:60°
10. 三角形的三个内角的度数之比为 $1:2:3$,最大边长是 $8$ cm,则最小边长是(
A.$7$ cm
B.$4$ cm
C.$7.5$ cm
D.$3$ cm
B
)A.$7$ cm
B.$4$ cm
C.$7.5$ cm
D.$3$ cm
答案:
B
11. 如图,在 $Rt\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$CD$ 是斜边 $AB$ 上的高,$\angle ACD = 30^{\circ}$,那么下列结论正确的是(
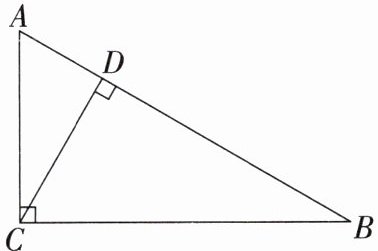
A.$AD= \frac{1}{2}CD$
B.$AC= \frac{1}{2}AB$
C.$BD= \frac{1}{2}BC$
D.$CD= \frac{1}{2}AB$
B
)
A.$AD= \frac{1}{2}CD$
B.$AC= \frac{1}{2}AB$
C.$BD= \frac{1}{2}BC$
D.$CD= \frac{1}{2}AB$
答案:
解析:选 B. 因为∠ADC=90°,∠ACD=30°,所以 AD= $\frac{1}{2}$AC,故 A 错误;因为∠ACD+∠A=90°,∠B+∠A=90°,所以∠ACD=∠B=30°,所以 AC= $\frac{1}{2}$AB,故 B 正确;BD≠$\frac{1}{2}$BC,CD= $\frac{1}{2}$BC,故 C,D 错误.故选 B.
12. 如图,直线 $m// n$,等边 $\triangle ABC$ 的顶点 $B$ 在直线 $n$ 上,$\angle 2 = 35^{\circ}$,则 $\angle 1$ 的度数为(
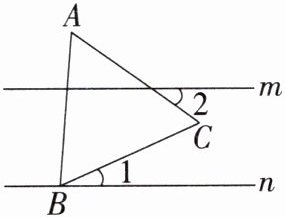
A.$40^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$35^{\circ}$
B
)
A.$40^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$35^{\circ}$
答案:
B
13. 如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$BC = 24$,将其沿 $AD$ 折叠,使点 $C$ 落在 $AB$ 上的点 $E$ 处,折痕为 $AD$,则 $DE$ 的长是(

A.$12$
B.$10$
C.$8$
D.$6$
8
)
A.$12$
B.$10$
C.$8$
D.$6$
答案:
解析:选 C. 由翻折的性质,可知∠AED=∠C=90°,DE=CD,所以∠BED=∠AED=90°.又因为∠B=30°,所以 DE= $\frac{1}{2}$BD,所以 CD+BD=DE+BD=3DE=BC.因为 BC=24,所以 DE=8.故选 C.
14. 如图,已知 $\triangle ABC$ 与 $\triangle CDE$ 都是等边三角形,点 $B$,$C$,$D$ 在同一条直线上,$AD$ 与 $BE$ 相交于点 $G$,$BE$ 与 $AC$ 相交于点 $F$,$AD$ 与 $CE$ 相交于点 $H$,连接 $FH$.给出下列结论:①$\triangle ACD\cong\triangle BCE$;②$\triangle AGB = 60^{\circ}$;③$BF = AH$;④$\triangle CFH$ 是等边三角形.其中正确结论的个数是(

A.$1$
B.$2$
C.$3$
D.$4$
D
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:
解析:选 D. 因为△ABC 与△CDE 都是等边三角形,所以∠BCA=∠DCE=60°,AC=BC,CE=CD,所以∠BCE=∠ACD.在△BCE 和△ACD 中,$\begin{cases} BC=AC, \\ ∠BCE=∠ACD, \\ CE=CD, \end{cases}$所以△BCE≌△ACD(SAS),故①正确.因为△BCE≌△ACD,所以∠CBF=∠CAH.又因为∠BFC=∠AFG,所以∠AGB=∠ACB=60°,故②正确.因为∠BCA=∠DCE=60°,所以∠ACE=60°.在△BCF 和△ACH 中,$\begin{cases} ∠CBF=∠CAH, \\ BC=AC, \\ ∠BCF=∠ACH, \end{cases}$所以△BCF≌△ACH(ASA),所以 CF=CH,BF=AH,故③正确.因为 CF=CH,∠ACH=60°,所以△CFH 是等边三角形,故④正确.故选 D.
15. 如图,$\triangle ABC$ 是等边三角形,在 $AC$ 边的右侧作等腰 $Rt\triangle ACD$,$\angle ACD = 90^{\circ}$,连接 $BD$,则 $\angle ADB$ 的度数为
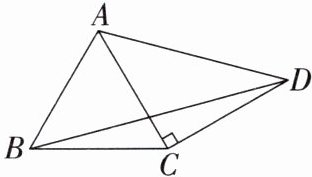
30°
.
答案:
30°
16. 某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价 $a$ 元,则购买这种草皮至少需要

150a
元.
答案:
150a
查看更多完整答案,请扫码查看


