1.
斜边
和一直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL
”).
答案:
斜边 HL
2. 下列关于两个直角三角形全等的判定,不正确的是(
A.斜边和一锐角分别相等的两个直角三角形全等
B.两条直角边分别相等的两个直角三角形全等
C.斜边和一直角边分别相等的两个直角三角形全等
D.两个面积相等的直角三角形全等
D
)A.斜边和一锐角分别相等的两个直角三角形全等
B.两条直角边分别相等的两个直角三角形全等
C.斜边和一直角边分别相等的两个直角三角形全等
D.两个面积相等的直角三角形全等
答案:
D
3. 如图,$BE= CF,AE⊥BC,DF⊥BC$,要根据“HL”证明$Rt△ABE\cong Rt△DCF$,则还需要添加一个条件是(
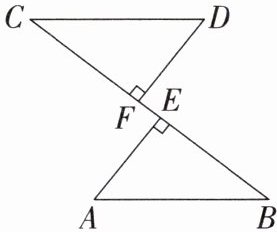
A.$AE= DF$
B.$∠A= ∠D$
C.$∠B= ∠C$
D.$AB= DC$
D
)
A.$AE= DF$
B.$∠A= ∠D$
C.$∠B= ∠C$
D.$AB= DC$
答案:
解析:选D.添加条件AB=DC.
理由:因为AE⊥BC,DF⊥BC,
所以∠AEB=∠CFD=90°.
在Rt△ABE和Rt△DCF中,{AB=DC, BE=CF},所以Rt△ABE≌Rt△DCF(HL).
故选D.
理由:因为AE⊥BC,DF⊥BC,
所以∠AEB=∠CFD=90°.
在Rt△ABE和Rt△DCF中,{AB=DC, BE=CF},所以Rt△ABE≌Rt△DCF(HL).
故选D.
4. 如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,这两个滑梯与地面夹角中$∠ABC= 32^{\circ }$,则$∠DFE$的度数是(
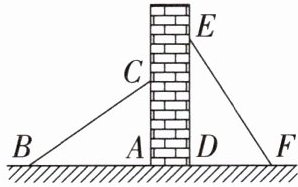
A.$32^{\circ }$
B.$62^{\circ }$
C.$58^{\circ }$
D.$68^{\circ }$
C
)
A.$32^{\circ }$
B.$62^{\circ }$
C.$58^{\circ }$
D.$68^{\circ }$
答案:
解析:选C.在Rt△ABC和Rt△DEF中,{BC=EF, AC=DF},
所以Rt△ABC≌Rt△DEF(HL),
所以∠DEF=∠ABC=32°,
所以∠DFE=90°-32°=58°.
故选C.
所以Rt△ABC≌Rt△DEF(HL),
所以∠DEF=∠ABC=32°,
所以∠DFE=90°-32°=58°.
故选C.
5. 如图,在$Rt△ABC$的斜边AB上截取$AD= AC$,过点D作$DE⊥AB$交BC于点E,则有(
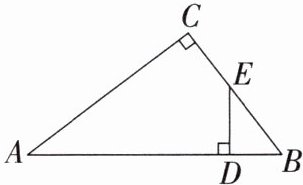
A.$DE= DB$
B.$DE= CE$
C.$CE= BE$
D.$CE= BD$
B
)
A.$DE= DB$
B.$DE= CE$
C.$CE= BE$
D.$CE= BD$
答案:
B
6. 用三角尺可按下面方法画角平分线:在已知的$∠AOB$的两边上,分别取$OM= ON$,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分$∠AOB$.作法中用到证明$△OMP与△ONP$全等的判定方法是(
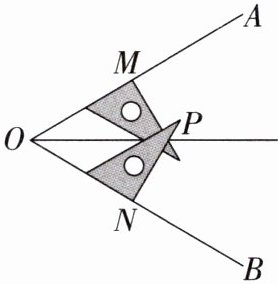
A.SAS
B.SSS
C.ASA
D.HL
D
)
A.SAS
B.SSS
C.ASA
D.HL
答案:
D
7. 如图,已知AD,CE是$△ABC$的两条高线,$AD= CE,∠CAD= 25^{\circ }$,则$∠OCD= $
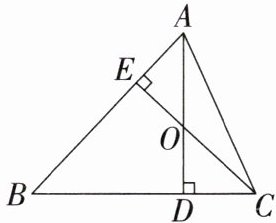
40
度.
答案:
40
8. 如图,在$△ABC和△ADE$中,$∠ACB= ∠ADE= 90^{\circ },AB= AE,∠1= ∠2$,线段BC的延长线交DE于点F,连接AF.若$S_{△ABF}= 14,AD= 4,CF= \frac {5}{4}$,则线段EF的长度为
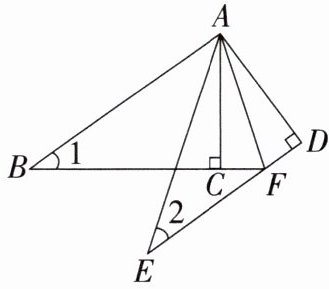
$\frac{9}{2}$
.
答案:
$\frac{9}{2}$
查看更多完整答案,请扫码查看


