《2025年新坐标同步练习八年级数学上册人教版青海专用》

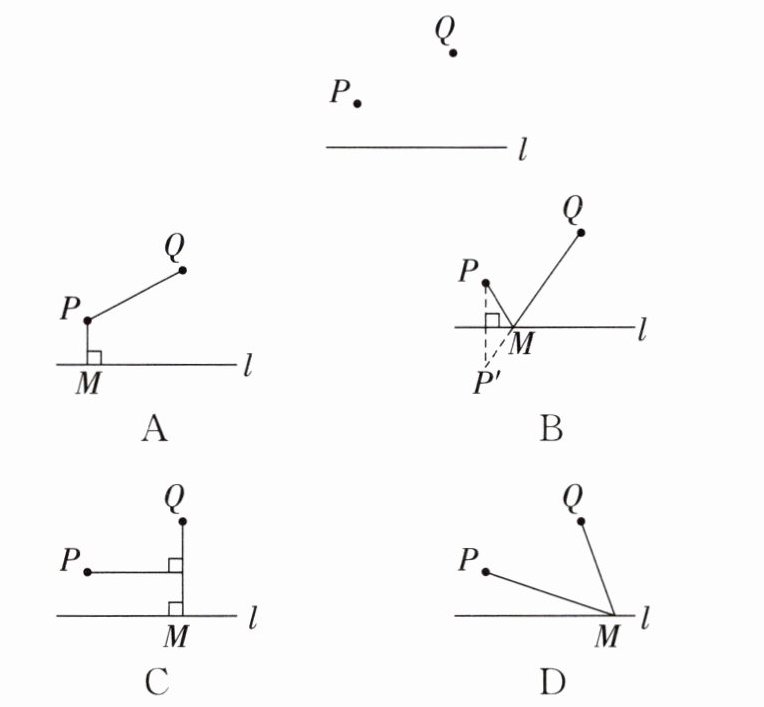
1. 如图,直线 $ l $ 是一条河,$ P $,$ Q $ 两地相距 $ 5.75 \mathrm{km} $,$ P $,$ Q $ 两地到 $ l $ 的距离分别为 $ 2.5 \mathrm{km} $,$ 5 \mathrm{km} $,欲在 $ l $ 上的某点 $ M $ 处修建一个水泵站,向 $ P $,$ Q $ 两地供水. 现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是(B)

 

答案： B

2. 如图,在 $ \mathrm{Rt} \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC = 6 $,$ BC = 8 $,$ AB = 10 $. 如果 $ D $,$ E $ 分别为 $ BC $,$ AB $ 上的动点,那么 $ AD + DE $ 的最小值是( )


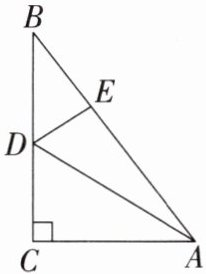
A.$ 8.4 $
B.$ 9.6 $
C.$ 10 $
D.$ 10.8 $

答案：
解析:选B.如图，作点A关于BC的对称点A',过点A'作A'E⊥AB,交BC于点D,连接A'B,AD,
　　　　　
则AD=A'D,
所以AD+DE=A'D+DE≥A'E,
即AD+DE的最小值为A'E.
因为AC=6,
所以AA'=12.
因为∠ACB=90°,
所以$S_{△AA'B}= \frac{1}{2}·AA'·BC= \frac{1}{2}·AB·A'E,$
又因为BC=8,AB=10,
所以$A'E= \frac{AA'·BC}{AB}= \frac{12×8}{10}=9.6,$
即AD+DE的最小值为9.6.
故选B.

3. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,直线 $ EF $ 是边 $ AB $ 的垂直平分线,$ D $ 是边 $ BC $ 的中点,$ M $ 是 $ EF $ 上一个动点,$ \triangle ABC $ 的面积为 $ 12 $,$ BC = 4 $,则 $ \triangle BDM $ 周长的最小值是______.

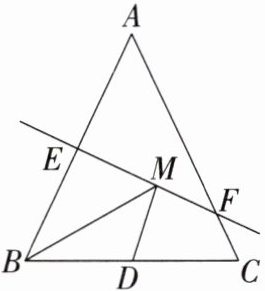
答案：
解析:连接AD.
　　　　　　
因为△ABC是等腰三角形，D是边BC的中点，
所以AD⊥BC，
所以$S_{△ABC}= \frac{1}{2}BC·AD= \frac{1}{2}×4·AD=12,$解得AD=6.
因为EF是边AB的垂直平分线，
所以点B关于直线EF的对称点为点A，
所以AD的长为BM十MD的最小值，
所以△BDM周长的最小值$=(BM+MD)+BD=AD+ \frac{1}{2}BC=6+ \frac{1}{2}×4=6+2=8.$
答案:8

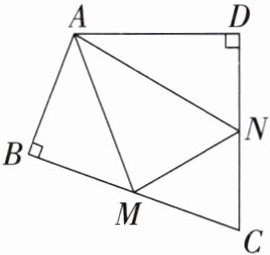
4. 如图,在四边形 $ ABCD $ 中,$ \angle BAD = 110^{\circ} $,$ \angle B = \angle D = 90^{\circ} $,在 $ BC $,$ CD $ 上分别找一点 $ M $,$ N $,使 $ \triangle AMN $ 的周长最小,则 $ \angle AMN + \angle ANM $ 的度数为140°.

答案： 140°

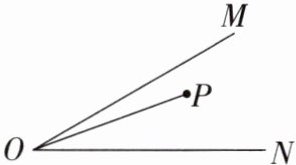
5. 如图,已知 $ \angle MON = 30^{\circ} $,在 $ \angle MON $ 的内部有一点 $ P $,$ A $ 为 $ OM $ 上一动点,$ B $ 为 $ ON $ 上一动点,$ OP = 6 $,当 $ \triangle PAB $ 的周长最小时,$ \angle APB = $______,$ \triangle PAB $ 的周长的最小值是______.

答案：
解析:如图，分别作点P关于OM,ON的对称点P',P";连接P'P",分别交OM,ON于点A,B,连接PA,PB,则此时△PAB的周长最小.
连接OP',OP".
　　　　　　
由轴对称的性质，得OP=OP'=OP"=6,∠P'OA=∠POA,∠P"OB=∠POB,
∠AP'O=∠APO,∠BP"O=∠BPO.
因为∠MON=30°,
所以∠P'OP"=2∠MON=60°,
所以△P'OP"是等边三角形，
所以P'P"=OP=6,∠AP'O=∠BP"O=60°,所以△PAB的周长=P'P"=6,∠APB=∠AP'O+∠BP"O=120°.
答案:120°　6

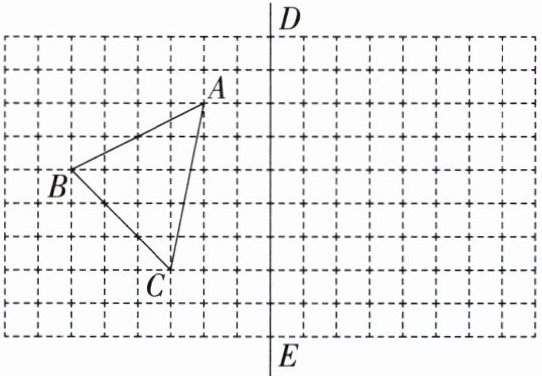
6. 如图,所给网格图中每小格均为边长是 $ 1 $ 的正方形,$ \triangle ABC $ 的顶点均在格点上. 请完成下列各题：(用直尺画图)
(1)画出 $ \triangle ABC $ 关于直线 $ DE $ 对称的 $ \triangle A_1B_1C_1 $；
(2)在 $ DE $ 上画出点 $ P $,使 $ PB + PC $ 最小；
(3)在 $ DE $ 上画出点 $ Q $,使 $ QA + QC $ 最小.

答案：
解:
(1)△A1B1C1如图所示.
　　　
(2)点P如图所示.
(3)点Q如图所示.