《2025年新坐标同步练习八年级数学上册人教版青海专用》

1. 两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).

答案： 相等 SAS

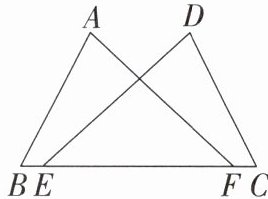
2. 如图,点E,F在BC上,BE= CF,∠B= ∠C,用“SAS”证明△ABF≌△DCE,还需添加的条件为(A)

A.AB= DC
B.AF= DE
C.∠A= ∠D
D.∠AFB= ∠DEC

答案： A

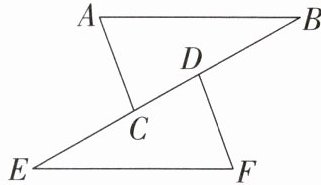
3. 如图,AC= DF,BD= EC,AC//DF,∠ACB= 80°,∠B= 30°,则∠F= (C)

A.60°
B.65°
C.70°
D.80°

答案： C

4. 使△ABC≌△A'B'C'的条件是(D)
A.AB= A'B',∠B= ∠B',AC= A'C'
B.AB= A'B',∠A= ∠A',BC= B'C'
C.AC= A'C',∠B= ∠B',BC= B'C'
D.AC= A'C',∠C= ∠C',CB= C'B'

答案： D

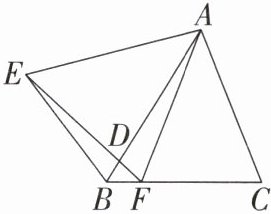
5. 如图,在△ABC与△AEF中,AB= AE,BC= EF,∠ABC= ∠AEF,∠EAB= 42°,AB交EF于点D,连接EB.下列结论：
①∠FAC= 42°；②AF= AC；③∠EFB= 42°；④AD= AC.其中正确的个数为(B)

A.4
B.3
C.2
D.1

答案： B

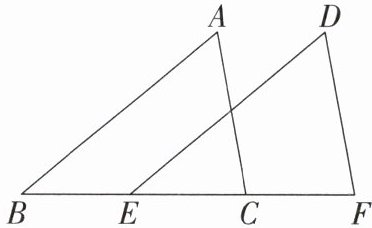
6. 如图,点B,E,C,F在一条直线上,AB//DE,且AB= DE,请添加一个条件BE=CF(答案不唯一),使△ABC≌△DEF.

答案： BE=CF(答案不唯一)

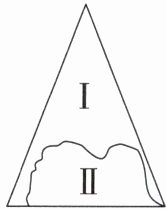
7. 如图,一块三角形玻璃碎成了Ⅰ和Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第Ⅰ块玻璃碎片.

答案： Ⅰ

8. 完成下面的证明过程.
已知：为测量A,B间的距离,施工队设计了如图所示的方案,其中CD= CA,CE= CB,且点A,C,D和点B,C,E分别在同一条直线上.
求证：DE= AB.
证明：在△DEC和△ABC中,
CD=CA,
∠DCE=∠ACB(对顶角相等),
CE=CB,
所以△DEC≌△ABC(SAS).
所以DE= AB(全等三角形的对应边相等).

答案： CA DCE ACB 对顶角相等 CB SAS 全等三角形的对应边相等