《2025年新坐标同步练习八年级数学上册人教版青海专用》

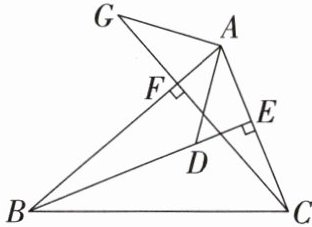
5. 如图,在$△ABC$中,$BE$,$CF分别是AC$,$AB$边上的高,在$BE上取一点D$,使$DB = AC$,在射线$CF上取一点G$,使$GC = AB$,连接$AD$,$AG$。若$∠DAE = 37^{\circ}$,$∠ABE = 18^{\circ}$,求$∠G$的度数。

答案： 解:因为BE，CF分别是AC，AB边上的高，所以∠BEA=∠CFA=90°.所以∠ABD+∠BAC=90°，∠GCA+∠BAC=90°.所以∠ABD=∠GCA.在△ABD和△GCA中，{DB=AC，∠ABD=∠GCA，AB=GC，所以△ABD≌△GCA(SAS).所以∠BAD=∠G.因为∠BAD=180°-90°-∠ABE-∠DAE=90°-18°-37°=35°，所以∠G=35°.

6. 如图,在$△ABC$中,$AD ⊥ BC于点D$,$BE ⊥ AC于点E$,$AD与BE相交于点F$。若$BF = AC$,求证：$△ADC ≌ △BDF$。

答案： 证明:因为AD⊥BC，BE⊥AC，所以∠ADC=∠BDF=∠BEA=90°.因为∠AFE=∠BFD，∠DAC+∠AEF+∠AFE=180°，∠BDF+∠BFD+∠DBF=180°，所以∠DAC=∠DBF.在△ADC和△BDF中，{∠ADC=∠BDF，∠DAC=∠DBF，AC=BF，所以△ADC≌△BDF(AAS).

7. 如图,在$△ABC$中,$AB = AC$,$∠BAC = 90^{\circ}$,分别过点$B$,$C向过点A$的直线作垂线,垂足分别为$E$,$F$。
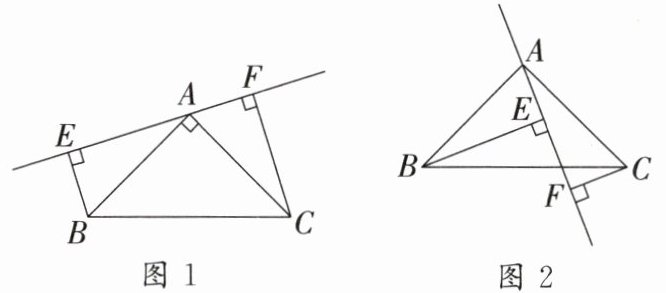
(1)如图 1,过点$A的直线与斜边BC$不相交时,求证：$EF = BE + CF$；
(2)如图 2,过点$A的直线与斜边BC$相交时,其他条件不变。若$BE = 10$,$CF = 4.5$,求$EF$的长。

答案：
(1)证明:因为BE⊥EA，CF⊥AF，所以∠BAC=∠BEA=∠CFE=90°，所以∠EAB+∠CAF=90°，∠EBA+∠EAB=90°，所以∠CAF=∠EBA.在△BEA和△AFC中，{∠BEA=∠AFC=90°，∠EBA=∠CAF，AB=AC，所以△BEA≌△AFC(AAS)，所以AE=CF，BE=AF，所以EF=AF+AE=BE+CF.
(2)因为BE⊥EA，CF⊥AF，所以∠BAC=∠BEA=∠CFE=90°，所以∠EAB+∠CAF=90°，∠ABE+∠EAB=90°，所以∠CAF=∠ABE.在△BEA和△AFC中，{∠BEA=∠AFC=90°，∠EBA=∠CAF，AB=AC，所以△BEA≌△AFC(AAS)，所以EA=FC=4.5，BE=AF=10，所以EF=AF-AE=10-4.5=5.5.