《2025年新坐标同步练习八年级数学上册人教版青海专用》

1. 等腰三角形的两个底角相等.

答案： 相等

2. 如图,已知 $ DE // BC $,$ AB = AC $,$ \angle 1 = 125^{\circ} $,则 $ \angle C $ 的度数是(A)


A.$ 55^{\circ} $
B.$ 45^{\circ} $
C.$ 35^{\circ} $
D.$ 65^{\circ} $

答案： A

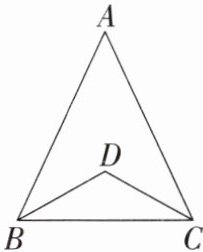
3. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ \triangle ABC $ 内一点,且 $ BD = DC $.求证：$ \angle ABD = \angle ACD $.

答案： 证明:因为AB=AC,
所以∠ABC=∠ACB.
因为BD=CD,所以∠DBC=∠DCB,
所以∠ABC-∠DBC=∠ACB-∠DCB,
即∠ABD=∠ACD.

4. 等腰三角形底边上的中线、高及顶角平分线重合.

答案： 重合

5. 下列说法错误的是(A)

A.等腰三角形的高、中线、角平分线重合
B.三角形两边的垂直平分线的交点到三个顶点的距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的 2 倍

答案： 解析:选A.A.等腰三角形底边上的高、中线、顶角的平分线重合,故A错误;B.三角形两边的垂直平分线的交点到三个顶点的距离相等,故B正确;C.等腰三角形的两个底角相等,故C正确;D.等腰三角形顶角的外角是底角的2倍,故D正确.故选A.

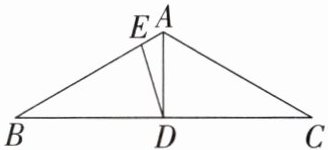
6. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle BAC = 120^{\circ} $,$ AD $ 是 $ BC $ 边上的中线,且 $ BD = BE $,计算 $ \angle ADE $ 的度数.

答案： 解:因为AB=AC,∠BAC=120°,
所以∠B=∠C=$\frac{1}{2}$×(180°-∠BAC)=30°.
因为BD=BE,
所以∠BDE=∠BED=$\frac{1}{2}$×(180°-∠B)=75°.
因为AB=AC,AD是BC边上的中线,
所以AD⊥BC,
所以∠ADB=90°,
所以∠ADE=∠ADB-∠BDE=15°.

7. 有两个角相等的三角形是等腰三角形(简写成“等角对等边”).

答案： 相等

8. 下列能确定 $ \triangle ABC $ 是等腰三角形的是(A)
A.$ \angle A = 50^{\circ} $,$ \angle B = 80^{\circ} $
B.$ \angle A = 42^{\circ} $,$ \angle B = 48^{\circ} $
C.$ \angle A = 2\angle B = 70^{\circ} $
D.$ AB = 4 $,$ BC = 5 $,周长为 15

答案： 解析:选A.A.因为∠A=50°,∠B=80°,所以∠C=180°-∠A-∠B=50°,所以∠A=∠C,所以△ABC是等腰三角形,故本选项能确定△ABC是等腰三角形;
B.因为∠A=42°,∠B=48°,所以∠C=180°-∠A-∠B=90°,所以∠A≠∠B≠∠C,所以△ABC不是等腰三角形,故本选项能确定△ABC不是等腰三角形;
C.因为∠A=2∠B=70°,所以∠B=35°,所以∠C=180°-∠A-∠B=75°,所以∠A≠∠B≠∠C,所以△ABC不是等腰三角形,故本选项能确定△ABC不是等腰三角形;
D.因为AB=4,BC=5,周长为15,所以AC=15-4-5=6,所以AB≠BC≠AC,所以△ABC不是等腰三角形,故本选项能确定△ABC不是等腰三角形.
故选A.

9. 若等腰三角形的周长为 10 cm,其中一边长为 2 cm,则该等腰三角形的底边长为(A)
A.2 cm
B.4 cm
C.6 cm
D.8 cm

答案： A

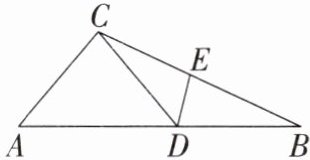
10. 如图,在 $ \triangle ABC $ 中,$ D $ 为 $ AB $ 上一点,$ E $ 为 $ BC $ 上一点,且 $ AC = CD = BD = BE $,$ \angle A = 50^{\circ} $,则 $ \angle CDE $ 的度数为(D)


A.$ 50^{\circ} $
B.$ 51^{\circ} $
C.$ 51.5^{\circ} $
D.$ 52.5^{\circ} $

答案： D