例(教材P76)在等号左边添上合适的运算符号和括号,使计算结果等于右边的数。
3○3○3○3= 1
3○3○3○3= 2
3○3○3○3= 3
3○3○3○3= 4
3○3○3○3= 5
3○3○3○3= 6
3○3○3○3= 7
3○3○3○3= 8
思路分析
解决这类问题,要在牢记运算规则和顺序的基础上,从算式的得数出发,运用分析法和尝试法逐步解决。如下表所示:
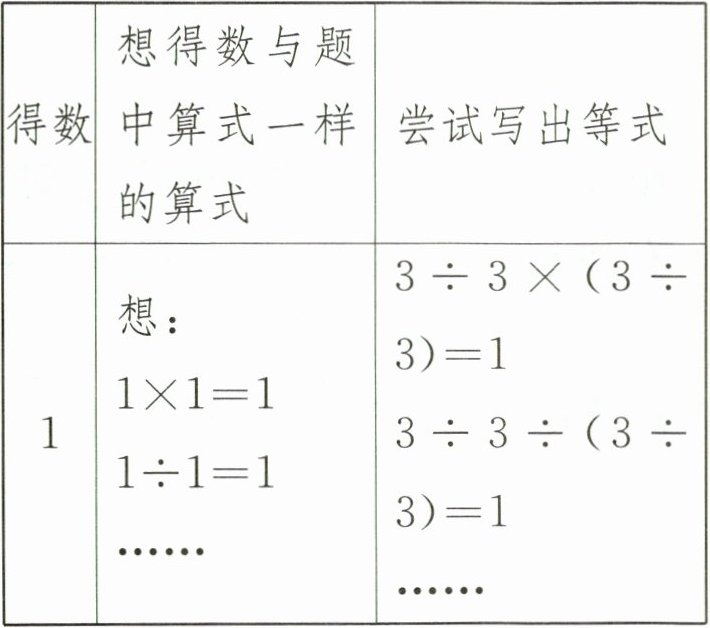
| 得数 | 想得数与题中算式一样的算式 | 尝试写出等式 |
| :--- | :------------------------- | :------------------------- |
| 1 | 想:1×1= 11÷1= 1…… | 3÷3×(3÷3)= 13÷3÷(3÷3)= 1…… |
| 2 | 想1+1= 2…… | 3÷3+3÷3= 2…… |
| 3 | 想9÷3= 3…… | (3+3+3)÷3= 3…… |
| 4 | 想12÷3= 4…… | (3×3+3)÷3= 4…… |
| 5 | 想3+2= 5…… | 3+(3+3)÷3= 5 …… |
| 6 | 想6×1= 6…… | (3+3)×(3÷3)= 6 …… |
| 7 | 想6+1= 7…… | 3+3+3÷3= 7 …… |
| 8 | 想9-1= 8…… | 3×3-3÷3= 8…… |

解答:答案不唯一,如:3÷3×(3÷3)= 1
3÷3+3÷3= 2
(3+3+3)÷3= 3
(3×3+3)÷3= 4
3+(3+3)÷3= 5
(3+3)×(3÷3)= 6
3+3+3÷3= 7
3×3-3÷3= 8
归纳点拨
解决这类问题,首先要牢记运算规则:没有括号的算式,先算乘除法,后算加减法;有括号的算式,先算括号里面的;同一级的要按从左往右的顺序依次计算,其次可以从算式的结果出发,采用分析法和尝试法解决。通常得数比较大的算式添“+”和“×”多一些,得数比较小的算式添“-”和“÷”多一些。
3○3○3○3= 1
3○3○3○3= 2
3○3○3○3= 3
3○3○3○3= 4
3○3○3○3= 5
3○3○3○3= 6
3○3○3○3= 7
3○3○3○3= 8
思路分析
解决这类问题,要在牢记运算规则和顺序的基础上,从算式的得数出发,运用分析法和尝试法逐步解决。如下表所示:

| 得数 | 想得数与题中算式一样的算式 | 尝试写出等式 |
| :--- | :------------------------- | :------------------------- |
| 1 | 想:1×1= 11÷1= 1…… | 3÷3×(3÷3)= 13÷3÷(3÷3)= 1…… |
| 2 | 想1+1= 2…… | 3÷3+3÷3= 2…… |
| 3 | 想9÷3= 3…… | (3+3+3)÷3= 3…… |
| 4 | 想12÷3= 4…… | (3×3+3)÷3= 4…… |
| 5 | 想3+2= 5…… | 3+(3+3)÷3= 5 …… |
| 6 | 想6×1= 6…… | (3+3)×(3÷3)= 6 …… |
| 7 | 想6+1= 7…… | 3+3+3÷3= 7 …… |
| 8 | 想9-1= 8…… | 3×3-3÷3= 8…… |

解答:答案不唯一,如:3÷3×(3÷3)= 1
3÷3+3÷3= 2
(3+3+3)÷3= 3
(3×3+3)÷3= 4
3+(3+3)÷3= 5
(3+3)×(3÷3)= 6
3+3+3÷3= 7
3×3-3÷3= 8
归纳点拨
解决这类问题,首先要牢记运算规则:没有括号的算式,先算乘除法,后算加减法;有括号的算式,先算括号里面的;同一级的要按从左往右的顺序依次计算,其次可以从算式的结果出发,采用分析法和尝试法解决。通常得数比较大的算式添“+”和“×”多一些,得数比较小的算式添“-”和“÷”多一些。
答案:
- $3÷3×(3÷3)=1$
$3÷3 + 3÷3=2$
$(3 + 3 + 3)÷3=3$
$(3×3 + 3)÷3=4$
$3+(3 + 3)÷3=5$
$(3 + 3)×(3÷3)=6$
$3 + 3+3÷3=7$
$3×3-3÷3=8$
$3÷3 + 3÷3=2$
$(3 + 3 + 3)÷3=3$
$(3×3 + 3)÷3=4$
$3+(3 + 3)÷3=5$
$(3 + 3)×(3÷3)=6$
$3 + 3+3÷3=7$
$3×3-3÷3=8$
查看更多完整答案,请扫码查看


