第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
6. 小明用天平测量一铁块的质量,他先把游码拨在标尺的正中央对着0.5g的刻度线上,然后旋动横梁右端的螺母,使天平横梁平衡.在天平左盘放上铁块,在天平右盘上放50g砝码一只、2g砝码一只,且将游码拨到0.3g刻度线处时,天平再次平衡.则铁块的质量为(
A.51.8g
B.52.3g
C.52.5g
D.52.8g
A
).A.51.8g
B.52.3g
C.52.5g
D.52.8g
答案:
A
7. 一蜡块悬浮在酒精和水的混合液中,这时蜡块受到的浮力为$F_1.$若向混合液中加入一些水,蜡块静止时受到的浮力为$F_2,$则(
$A. F_1>F_2$
$B. F_1= F_2$
$C. F_1<F_2$
D. 不能确定
B
).$A. F_1>F_2$
$B. F_1= F_2$
$C. F_1<F_2$
D. 不能确定
答案:
B [解析]蜡块原本悬浮在混合液中,说明蜡块和混合液平均密度相同,蜡块受到的浮力和蜡块重力相等,向混合液中加入一些水后,混合液的密度变大,大于蜡块的密度,蜡块将要上浮至液面呈漂浮状态,这时蜡块受到的浮力仍然和自身重力相等,所以蜡块两次所受浮力相等,即 $ F_1 = F_2 $。
8. 如图所示,甲、乙两容器间用一细管相连,在细管上有一阀门K将两容器分开.现在甲中装水,乙中装浓盐水,且使两容器液面相平,然后打开阀门K,则斜管中液体的流动情况是(
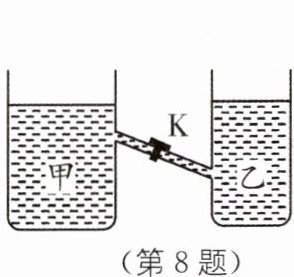
A.由甲向乙流
B.由乙向甲流
C.静止不动
D.先向乙流,后向甲流
B
).
A.由甲向乙流
B.由乙向甲流
C.静止不动
D.先向乙流,后向甲流
答案:
B [解析]当阀门 K 打开时,可在阀门 K 处选取一“液片”进行研究,分析“液片”的受力情况,通过“液片”的运动情况,判断出液体的流动方向.阀门打开后,“液片”的左侧受到水向右的压力 $ F_1 = p_1 S_1 $,同时“液片”的右侧受到盐水向左的压力 $ F_2 = p_2 S_2 $.因“液片”左侧为水、右侧为盐水(盐水的密度较大),且两侧液面高度相同,据 $ p = \rho gh $ 可知,“液片”右侧所受的压强较大,即 $ p_1 < p_2 $.又因“液片”左、右两侧面积相等,所以有 $ F_1 < F_2 $,即“液片”将由静止开始向左移动,故斜管中的液体将由乙向甲容器流动.
9. 如图所示,两个底面积不同的圆柱形容器A和B(Sₐ>Sᵦ),容器足够高,分别盛有甲、乙两种液体,且两种液体对容器底部的压强相等.若在A容器中倒入或抽出甲液体,在B容器中倒入或抽出乙液体,使两液体对容器底部的压力相等,则下列判断正确的是(
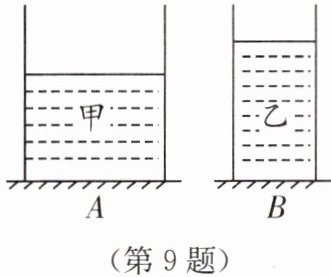
A.倒入的液体高度hₐ可能等于hᵦ
B.倒入的液体高度hₐ可能小于hᵦ
C.抽出的液体高度hₐ可能大于hᵦ
D.抽出的液体高度hₐ一定小于hᵦ
C
).
A.倒入的液体高度hₐ可能等于hᵦ
B.倒入的液体高度hₐ可能小于hᵦ
C.抽出的液体高度hₐ可能大于hᵦ
D.抽出的液体高度hₐ一定小于hᵦ
答案:
C [解析]因为 $ p_{甲} = p_{乙} $,可得 $ \frac{F_{甲}}{S_A} = \frac{F_{乙}}{S_B} $,又因为 $ S_A > S_B $,所以 $ F_{甲} > F_{乙} $。
由于圆柱形容器里面液体产生的压力与液体的重力相等,则容器内所装的甲液体的重力大于乙液体的重力,即 $ G_{甲} > G_{乙} $。
由 $ p_{甲} = p_{乙} $ 可得 $ \rho_{甲} gh_A = \rho_{乙} gh_B $,由图可知 $ h_A < h_B $,所以 $ \rho_{甲} > \rho_{乙} $。
设倒入或抽出液体后,压力变化量为 $ \Delta F $(等于液体重力变化量).
若倒入液体时,容器底所受压力为 $ F' = F + \Delta F $,要使压力相等,则 $ \Delta F_{甲} < \Delta F_{乙} $。
若抽出液体时,容器底所受压力为 $ F' = F - \Delta F $,要使压力相等,则 $ \Delta F_{甲} > \Delta F_{乙} $。
分两种情况讨论:
(1)倒入液体时,必须使 $ \Delta F_{甲} < \Delta F_{乙} $,就是 $ \rho_{甲} \Delta V_{甲} < \rho_{乙} \Delta V_{乙} $.因为 $ \rho_{甲} > \rho_{乙} $,所以 $ \Delta V_{甲} $ 必须小于 $ \Delta V_{乙} $.又因为 $ S_A > S_B $,所以 $ \Delta h_{甲} < \Delta h_{乙} $,即倒入的液体高度 $ h_{甲} $ 一定小于 $ h_{乙} $,故 A、B 错误.
(2)抽出液体时,必须使 $ \Delta F_{甲} > \Delta F_{乙} $,就是 $ \rho_{甲} \Delta V_{甲} > \rho_{乙} \Delta V_{乙} $.因为 $ \rho_{甲} > \rho_{乙} $,所以 $ \Delta V_{甲} $ 大于、小于、等于 $ \Delta V_{乙} $ 都可能.又因为 $ S_A > S_B $,所以又分为三种情况:
①若 $ \Delta V_{甲} = \Delta V_{乙} $,则 $ \Delta h_{甲} < \Delta h_{乙} $;
②若 $ \Delta V_{甲} > \Delta V_{乙} $,则 $ \Delta h_{甲} $ 可能大于或等于 $ \Delta h_{乙} $;
③若 $ \Delta V_{甲} < \Delta V_{乙} $,则 $ \Delta h_{甲} < \Delta h_{乙} $.
故 C 正确,D 错误.故选 C.
由于圆柱形容器里面液体产生的压力与液体的重力相等,则容器内所装的甲液体的重力大于乙液体的重力,即 $ G_{甲} > G_{乙} $。
由 $ p_{甲} = p_{乙} $ 可得 $ \rho_{甲} gh_A = \rho_{乙} gh_B $,由图可知 $ h_A < h_B $,所以 $ \rho_{甲} > \rho_{乙} $。
设倒入或抽出液体后,压力变化量为 $ \Delta F $(等于液体重力变化量).
若倒入液体时,容器底所受压力为 $ F' = F + \Delta F $,要使压力相等,则 $ \Delta F_{甲} < \Delta F_{乙} $。
若抽出液体时,容器底所受压力为 $ F' = F - \Delta F $,要使压力相等,则 $ \Delta F_{甲} > \Delta F_{乙} $。
分两种情况讨论:
(1)倒入液体时,必须使 $ \Delta F_{甲} < \Delta F_{乙} $,就是 $ \rho_{甲} \Delta V_{甲} < \rho_{乙} \Delta V_{乙} $.因为 $ \rho_{甲} > \rho_{乙} $,所以 $ \Delta V_{甲} $ 必须小于 $ \Delta V_{乙} $.又因为 $ S_A > S_B $,所以 $ \Delta h_{甲} < \Delta h_{乙} $,即倒入的液体高度 $ h_{甲} $ 一定小于 $ h_{乙} $,故 A、B 错误.
(2)抽出液体时,必须使 $ \Delta F_{甲} > \Delta F_{乙} $,就是 $ \rho_{甲} \Delta V_{甲} > \rho_{乙} \Delta V_{乙} $.因为 $ \rho_{甲} > \rho_{乙} $,所以 $ \Delta V_{甲} $ 大于、小于、等于 $ \Delta V_{乙} $ 都可能.又因为 $ S_A > S_B $,所以又分为三种情况:
①若 $ \Delta V_{甲} = \Delta V_{乙} $,则 $ \Delta h_{甲} < \Delta h_{乙} $;
②若 $ \Delta V_{甲} > \Delta V_{乙} $,则 $ \Delta h_{甲} $ 可能大于或等于 $ \Delta h_{乙} $;
③若 $ \Delta V_{甲} < \Delta V_{乙} $,则 $ \Delta h_{甲} < \Delta h_{乙} $.
故 C 正确,D 错误.故选 C.
10. 如图所示,在注有清水的试管内留有一稍大的空气泡,使太阳光从试管的正上方向下照,观察试管下方的白纸,可以发现白纸上与空气泡相对应的位置上,有一椭圆黑影,而其他部分竟是一条与试管平行的亮线.这是因为试管充满水的地方相当于
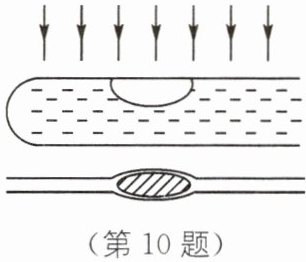
凸
透镜,而气泡与周边的水组成凹
透镜.如果把白纸从靠近试管向下移动到较远处,亮线的粗细将如何变化?先变细再变粗
.
答案:
凸 凹 先变细再变粗
11. 复印纸是现代办公的必备用品.某B4型号复印纸标有$“80g/m^2 257×364mm”$字样,一张该型号复印纸的质量大约为______g;一般情况下,一包复印纸共500张,聪明的小刘用刻度尺测出一包复印纸的厚度为5cm,从而推算出该复印纸的密度为$______kg/m^3.($保留一位有效数字)
11. 复印纸是现代办公的必备用品.某B4型号复印纸标有$“80g/m^2 257×364mm”$字样,一张该型号复印纸的质量大约为
11. 复印纸是现代办公的必备用品.某B4型号复印纸标有$“80g/m^2 257×364mm”$字样,一张该型号复印纸的质量大约为
7.5
g;一般情况下,一包复印纸共500张,聪明的小刘用刻度尺测出一包复印纸的厚度为5cm,从而推算出该复印纸的密度为$0.8 × 10^3
kg/m^3.($保留一位有效数字)
答案:
7.5 $ 0.8 × 10^3 $
12. 实验中有时需要将一束粗平行光变成细平行光,这可以利用两块透镜的组合来解决,试在图中的两个方框内各画出一种组合方式,分别写出两块透镜间的距离s跟两块透镜到各自焦点的距离$f_1、$$f_2$的关系.


答案:
如图所示

[解析]平行于主光轴的光线,经凸透镜后会聚到焦点;过焦点的光线经过凸透镜后平行于主轴.如图甲所示,可以用两个凸透镜,并使第一个透镜的右侧焦点跟第二个透镜的左侧焦点重合.为使出射的光线变细,应使第一个透镜的焦距 $ f_1 $ 大于第二个透镜的焦距 $ f_2 $,即 $ f_1 > f_2 $.此时,透镜间的距离 $ s = f_1 + f_2 $.如图乙所示,可以用一个凸透镜和一个凹透镜来组合.若使光线变细,就先用凸透镜使光线会聚,再让光线通过凹透镜发散,并使凸透镜的右侧焦点和凹透镜的右侧焦点重合.这时透镜间的距离 $ s = f_1 - f_2 $(其中 $ f_1 $ 为凸透镜的焦距, $ f_2 $ 为凹透镜的焦距).
如图所示

[解析]平行于主光轴的光线,经凸透镜后会聚到焦点;过焦点的光线经过凸透镜后平行于主轴.如图甲所示,可以用两个凸透镜,并使第一个透镜的右侧焦点跟第二个透镜的左侧焦点重合.为使出射的光线变细,应使第一个透镜的焦距 $ f_1 $ 大于第二个透镜的焦距 $ f_2 $,即 $ f_1 > f_2 $.此时,透镜间的距离 $ s = f_1 + f_2 $.如图乙所示,可以用一个凸透镜和一个凹透镜来组合.若使光线变细,就先用凸透镜使光线会聚,再让光线通过凹透镜发散,并使凸透镜的右侧焦点和凹透镜的右侧焦点重合.这时透镜间的距离 $ s = f_1 - f_2 $(其中 $ f_1 $ 为凸透镜的焦距, $ f_2 $ 为凹透镜的焦距).
查看更多完整答案,请扫码查看


