《2025年实验班提优训练暑假衔接版八升九年级物理苏科版》

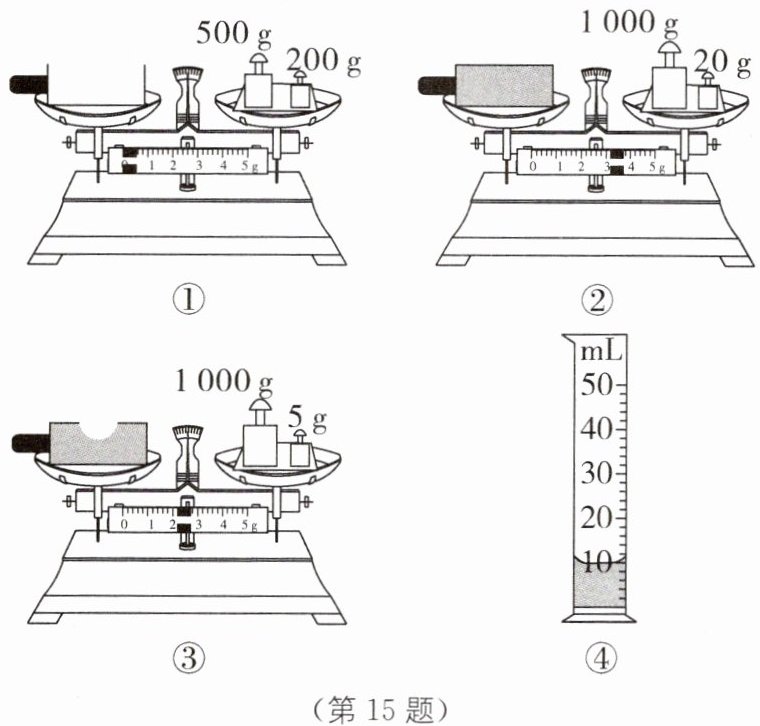
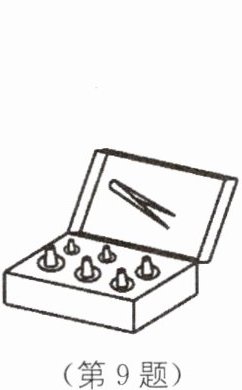
9. 物理实验中经常需要进行测量,如图所示是某架天平配套使用的砝码盒,盒内的砝码有 $ 100 \text{ g} $一个、 $ 50 \text{ g} $一个、 $ 20 \text{ g} $两个,剩下的砝码是10g一个和5g一个,调节好天平后,将物体放在右盘,通过加减砝码和移动游码使天平重新恢复了平衡,读出砝码和游码示数之和为 $ 112 \text{ g} $,则物体的实际质量是108g.

答案： 10g一个和5g一个 108

10. 小明测量石头挂件“福兔”的密度. 用天平测得它的质量为 $ 16.8 \text{ g} $,将它放入量筒并倒入适量的水,如图所示. 取出挂件,量筒中剩余水的体积为 $ 30 \text{ mL} $,则挂件的体积为______$ \text{cm}^3 $,密度为______$ \text{g/cm}^3 $,测得挂件的密度值与真实值相比______(填“偏大”“偏小”或“相同”).

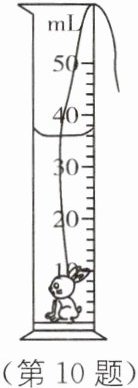
10. 小明测量石头挂件“福兔”的密度. 用天平测得它的质量为 $ 16.8 \text{ g} $,将它放入量筒并倒入适量的水,如图所示. 取出挂件,量筒中剩余水的体积为 $ 30 \text{ mL} $,则挂件的体积为6$ \text{cm}^3 $,密度为2.8$ \text{g/cm}^3 $,测得挂件的密度值与真实值相比偏小(填“偏大”“偏小”或“相同”).

答案： 6 2.8 偏小

11. 容积为 $ 250 \text{ mL} $的容器,装满水后的总质量为 $ 300 \text{ g} $,则容器质量为______g;若装满另一种液体后的总质量为 $ 250 \text{ g} $,则这种液体的密度为______ $ \text{g/cm}^3 $. ($ \rho_{\text{水}} = 1.0 × 10^{3} \text{ kg/m}^3 $)
11. 容积为 $ 250 \text{ mL} $的容器,装满水后的总质量为 $ 300 \text{ g} $,则容器质量为50g;若装满另一种液体后的总质量为 $ 250 \text{ g} $,则这种液体的密度为0.8 $ \text{g/cm}^3 $. ($ \rho_{\text{水}} = 1.0 × 10^{3} \text{ kg/m}^3 $)

答案： 50 0.8 [解析]本题考查密度公式及其变形公式的应用.由$ρ=\frac {m}{V}$得容器中水的质量$m_{水}=ρ_{水}V_{水}=1.0g/cm^{3}×250cm^{3}=250g$，则容器的质量为$m_{容}=m_{总}-m_{水}=300g-250g=50g$；液体的质量$m_{液}=m_{总}'-m_{容}=250g-50g=200g$，液体的体积$V_{液}=V_{水}=250cm^{3}$，则这种液体的密度$ρ_{液}=\frac {m_{液}}{V_{液}}=\frac {200g}{250cm^{3}}=0.8g/cm^{3}$.

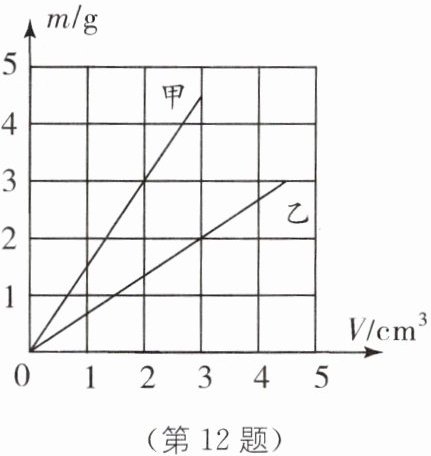
12. 甲、乙两种物质的质量与体积的关系图像如图所示,由图可知,其中密度较大的是甲(填“甲”或“乙”),甲的密度是1.5 $ \text{g/cm}^3 $.

答案： 甲 1.5

有 $ A $、$ B $、$ C $三个由同种材料制成的金属球,它们的质量分别为 $ 128 \text{ g} $、$ 400 \text{ g} $、$ 60 \text{ g} $,体积分别为 $ 16 \text{ cm}^3 $、$ 50 \text{ cm}^3 $、$ 12 \text{ cm}^3 $. 在 $ A $、$ B $、$ C $三个金属球中,若只有一个是空心的,那么______球是空心的,这种材料的密度为______.
答案：
有 $ A $、$ B $、$ C $三个由同种材料制成的金属球,它们的质量分别为 $ 128 \text{ g} $、$ 400 \text{ g} $、$ 60 \text{ g} $,体积分别为 $ 16 \text{ cm}^3 $、$ 50 \text{ cm}^3 $、$ 12 \text{ cm}^3 $. 在 $ A $、$ B $、$ C $三个金属球中,若只有一个是空心的,那么C球是空心的,这种材料的密度为$8g/cm^{3}$.

答案： C $8g/cm^{3}$

14. 小刚做测量蜡块密度的实验.

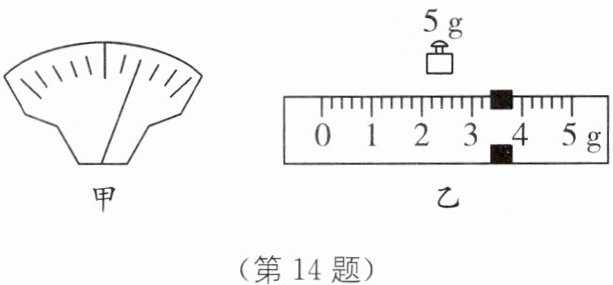
(1)将天平放在水平桌面上,移动游码至标尺的左端“0”刻度线处. 若此时指针的位置如图甲所示,应将平衡螺母向左移动,使天平平衡.
(2)将蜡块放在天平左盘中,另一盘所加砝码和游码位置如图乙所示时,天平平衡. 蜡块的质量为8.4g.
(3)将蜡块放入盛有 $ 50.0 \text{ mL} $水的量筒中,用铁丝将其压入水中,读得量筒的示数为 $ 60.0 \text{ mL} $,则该蜡块的体积为10.0 $ \text{cm}^3 $.
(4)计算得出蜡块的密度为$0.84×10^{3}$ $ \text{kg/m}^3 $.

答案：
(1)左端“0”刻度线 左
(2)左 8.4
(3)10.0
(4)$0.84×10^{3}$

15. 新情境 商鞅方升容积的测量 “商鞅方升”是上海博物馆的镇馆之宝,其容积是秦朝统一实施的体积标准——方升. 方升有多大呢? 小组同学对其复制品展开容积测量. 步骤如下:
①用天平测得空“商鞅方升”的质量;
②将“商鞅方升”内装入沙子直至沙子上表面与“商鞅方升”上表面齐平,测得“商鞅方升”与沙子的总质量;
③用小勺将沙子取出一部分装入量筒,测得“商鞅方升”与剩余沙子的总质量;
④测得量筒内沙子的体积.

(1)秦朝统一实施的体积标准——方升相当于现代的0.202L升?
(2)实验后,小明评价刚才的测量过程,认为步骤较多. 他设想:水的密度已知($ \rho_{\text{水}} = 1 × 10^{3} \text{ kg/m}^3 $),上述步骤中用水代替沙子,只要完成步骤①②(填上述步骤序号的一个或多个)就能测出“商鞅方升”的容积. 小组同学讨论后认为,小明的设想实际操作性不佳,表现在:“商鞅方升”中装满了水，放在天平上测量总质量时水容易溢出.

答案：
(1)0.202L
(2)①② “商鞅方升”中装满了水，放在天平上测量总质量时水容易溢出