《2025年通城学典课时作业本七年级数学上册浙教版》

19.有这样一道题：求$3x^{2}y+[2x^{2}y-(5x^{2}y^{2}-2y^{2})]-5(x^{2}y+y^{2}-x^{2}y^{2})$的值,其中$x= \frac{1}{2}$,$y= -1$.小明同学把“$x= \frac{1}{2}$”错看成“$x= -\frac{1}{2}$”,但计算结果是正确的；小华同学把“$y= -1$”错看成“$y= 1$”,但计算结果也是正确的.你知道其中的原因吗？请加以说明.

答案： $ 3x^{2}y+[2x^{2}y-(5x^{2}y^{2}-2y^{2})]-5(x^{2}y+y^{2}-x^{2}y^{2})=3x^{2}y+2x^{2}y-5x^{2}y^{2}+2y^{2}-5x^{2}y-5y^{2}+5x^{2}y^{2}=-3y^{2} $.所以计算结果与x的取值无关，且不论$ y=-1 $还是$ y=1 $，都有$ -3y^{2}=-3 $.所以小明同学和小华同学的计算结果都是正确的

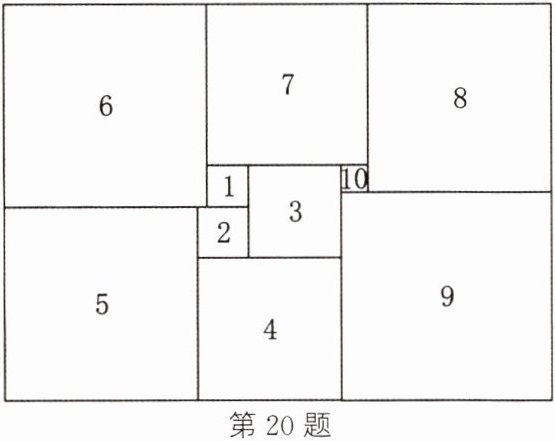
20.(2025·绍兴柯桥期末)如图,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,其中第1,2个正方形的边长分别为x,y.
(1)用含x,y的代数式填空：第3个正方形的边长为x+y；第5个正方形的边长为x+3y.
(2)当$y= 3$时,求第6个正方形的面积.因为第5个正方形的边长为$ x+3y $，所以第6个正方形的边长是$ (x+3y)+(y-x)=4y $.所以当$ y=3 $时，第6个正方形的边长为12.所以第6个正方形的面积为$ 12×12=144 $

答案：
(1) $ x+y $ $ x+3y $
(2) 因为第5个正方形的边长为$ x+3y $，所以第6个正方形的边长是$ (x+3y)+(y-x)=4y $.所以当$ y=3 $时，第6个正方形的边长为12.所以第6个正方形的面积为$ 12×12=144 $

21.(2025·杭州期中)【方法】有一种整式处理器,能将二次多项式处理成一次多项式,处理方法：将二次多项式的二次项系数与一次项系数的和(和为非零数)作为一次多项式的一次项系数,将二次多项式的常数项作为一次多项式的常数项.例如：$A= x^{2}+2x-3$,A经过处理器得到$B= (1+2)x-3= 3x-3$.
【应用】
若关于x的二次多项式A经过处理器得到B,根据以上方法,解决下面的问题：
(1)填空：若$A= 3x^{2}-2x+5$,则$B= $______x+5；
(2)若$A= 4x^{2}-5(2x-3)$,求关于x的方程$B= 9$的解.因为$ A=4x^{2}-5(2x-3)=4x^{2}-10x+15 $，所以A经过处理器得到$ B=(4-10)x+15=-6x+15 $.又因为$ B=9 $，所以$ -6x+15=9 $.由小学所学的解方程知识，可得$ x=1 $.所以关于x的方程$ B=9 $的解为$ x=1 $
【延伸】
(3)已知$M= x-2(m-4)x^{2}+7$,M是关于x的二次多项式,若N是M经过处理器得到的整式,满足$N= 3x+7$,求m的值.由题意，得$ m≠4 $.因为$ M=x-2(m-4)x^{2}+7 $，所以M经过处理器得到$ N=[-2(m-4)+1]x+7=(-2m+9)x+7 $.又因为$ N=3x+7 $，所以$ (-2m+9)x+7=3x+7 $.所以$ -2m+6=0 $.由小学所学的解方程知识，可得m的值为3

答案：
(1) $ x+5 $ 解析:因为$ A=3x^{2}-2x+5 $，所以A经过处理器得到$ B=(3-2)x+5=x+5 $.
(2) 因为$ A=4x^{2}-5(2x-3)=4x^{2}-10x+15 $，所以A经过处理器得到$ B=(4-10)x+15=-6x+15 $.又因为$ B=9 $，所以$ -6x+15=9 $.由小学所学的解方程知识，可得$ x=1 $.所以关于x的方程$ B=9 $的解为$ x=1 $
(3) 由题意，得$ m≠4 $.因为$ M=x-2(m-4)x^{2}+7 $，所以M经过处理器得到$ N=[-2(m-4)+1]x+7=(-2m+9)x+7 $.又因为$ N=3x+7 $，所以$ (-2m+9)x+7=3x+7 $.所以$ -2m+6=0 $.由小学所学的解方程知识，可得m的值为3