10. (2025·杭州滨江期末)下列各组数中,计算结果相等的是(
A.$-(-1)与-|-1|$
B.$-2^3与(-2)^3$
C.$\frac{3^2}{4}与(\frac{3}{4})^2$
D.$-3^2与(-3)^2$
B
)A.$-(-1)与-|-1|$
B.$-2^3与(-2)^3$
C.$\frac{3^2}{4}与(\frac{3}{4})^2$
D.$-3^2与(-3)^2$
答案:
B
11. 有下列算式:① $-(-2)^4= 16$;② $-5÷\frac{1}{5}= -5$;③ $\frac{2^3}{3}= \frac{8}{27}$;④ $-4^3= -12$;⑤ $(-3)^2×(-\frac{1}{3})= -3$.其中,错误的个数为(
A.2
B.3
C.4
D.5
C
)A.2
B.3
C.4
D.5
答案:
C
12. (新考向·数学文化)(2024·湖州南浔期末)我国古代《易经》一书中记载了一种“结绳计数”的方法:一女子在从右到左依次排列的绳子上打结,满七则向左进一.下列图示表示数 162 的是(
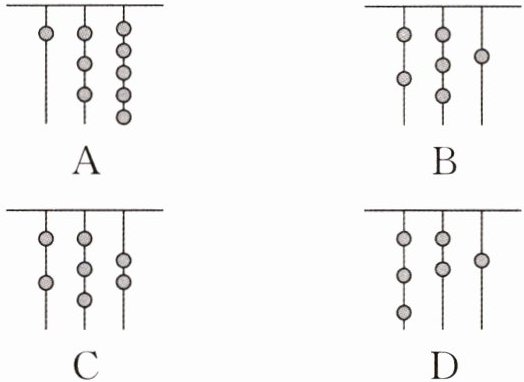
D
)
答案:
D 解析:A选项表示的数为$1×7^2+3×7+5=75$,故该选项错误.B选项表示的数为$2×7^2+3×7+1=120$,故该选项错误.C选项表示的数为$2×7^2+3×7+2=121$,故该选项错误.D选项表示的数为$3×7^2+2×7+1=162$,故该选项正确.
13. 如果一个数的立方等于 64,那么这个数是
4
.如果一个数的平方等于 64,那么这个数是±8
.
答案:
4,±8
14. 若$x,y满足|x+\frac{1}{5}|+(y-3\frac{1}{3})^2= 0$,则$x= $
$-\frac{1}{5}$
,$y= $$3\frac{1}{3}$
.
答案:
$-\frac{1}{5}$,$3\frac{1}{3}$
15. (教材 P60 作业题第 4 题变式)某种细胞开始时有 2 个,1 小时后分裂成 4 个并死去 1 个,2 小时后分裂成 6 个并死去 1 个,3 小时后分裂成 10 个并死去 1 个……按此规律,5 小时后细胞存活的个数是______
33
.
答案:
33 解析:根据题意,得1小时后分裂成4个并死去1个,剩3个,$3=2+1$;2小时后分裂成6个并死去1个,剩5个,$5=2^2+1$;3小时后分裂成10个并死去1个,剩9个,$9=2^3+1$……按此规律,5小时后细胞存活的个数是$2^5+1=33$.
16. (教材 P60 作业题第 3 题变式)计算:
(1)$-(-3)^4÷(-27)$;
(2)$(-3)^2×2-5×(-2)^3$;
(3)$(-1)^{2024}×(-3)^2×(-\frac{1}{2})^3$.
(1)$-(-3)^4÷(-27)$;
(2)$(-3)^2×2-5×(-2)^3$;
(3)$(-1)^{2024}×(-3)^2×(-\frac{1}{2})^3$.
答案:
(1)3;
(2)58;
(3)$-\frac{9}{8}$
(1)3;
(2)58;
(3)$-\frac{9}{8}$
17. (新考法·结论开放题)如图,拉面馆的师傅用 1 根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多根细的面条.第一次捏合后,可以拉出 2 根面条;第二次捏合后,可以拉出 4 根面条;第三次捏合后,可以拉出 8 根面条……
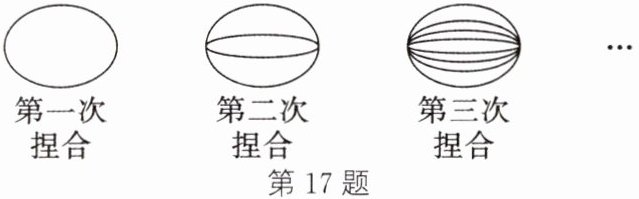
(1)第四次捏合后,可以拉出______根面条;第五次捏合后,可以拉出______根面条.
(2)第几次捏合后,可以拉出 128 根面条?可以拉出 200 根面条吗?
(1)
(2)

(1)第四次捏合后,可以拉出______根面条;第五次捏合后,可以拉出______根面条.
(2)第几次捏合后,可以拉出 128 根面条?可以拉出 200 根面条吗?
(1)
16
,32
;(2)
因为$128=2×2×2×2×2×2×2=2^7$,所以第7次捏合后,可以拉出128根面条 因为$200=2×2×2×5×5$,所以200不可以写成2的幂的形式.所以不可以拉出200根面条
答案:
(1)16,32;
(2)因为$128=2×2×2×2×2×2×2=2^7$,所以第7次捏合后,可以拉出128根面条 因为$200=2×2×2×5×5$,所以200不可以写成2的幂的形式.所以不可以拉出200根面条
(1)16,32;
(2)因为$128=2×2×2×2×2×2×2=2^7$,所以第7次捏合后,可以拉出128根面条 因为$200=2×2×2×5×5$,所以200不可以写成2的幂的形式.所以不可以拉出200根面条
查看更多完整答案,请扫码查看


