10. (教材 P103 作业题第 1 题变式)用代数式表示:
(1)比$a除以b$所得的商的 2 倍小 6 的数;
(2)$x的\frac{1}{3}$与 2 的和的算术平方根.
(1)比$a除以b$所得的商的 2 倍小 6 的数;
(2)$x的\frac{1}{3}$与 2 的和的算术平方根.
答案:
(1)$\frac{2a}{b}-6$ (2)$\sqrt{\frac{1}{3}x+2}$
11. 某市举行的歌手大赛今年共有$a$人参加,参赛的人数比去年增加 20%还多 3,则去年参赛的人数用含$a$的代数式表示为 (
A.$\frac{a + 3}{1 + 20\%}$
B.$(1 + 20\%)a + 3$
C.$\frac{a - 3}{1 + 20\%}$
D.$(1 + 20\%)a - 3$
C
)A.$\frac{a + 3}{1 + 20\%}$
B.$(1 + 20\%)a + 3$
C.$\frac{a - 3}{1 + 20\%}$
D.$(1 + 20\%)a - 3$
答案:
C
12. (新情境·日常生活)(2025·湖州德清期末)为鼓励和推广全民阅读活动,某书店开展促销活动,促销方法是将原价为$x元的一批图书以0.8(x - 12)$元的价格出售,下列说法中,能正确表达这批图书的促销方法的是(
A.在原价的基础上打 8 折后再减去 12 元
B.在原价的基础上打 0.8 折后再减去 12 元
C.在原价的基础上减去 12 元后再打 8 折
D.在原价的基础上减去 12 元后再打 0.8 折
C
)A.在原价的基础上打 8 折后再减去 12 元
B.在原价的基础上打 0.8 折后再减去 12 元
C.在原价的基础上减去 12 元后再打 8 折
D.在原价的基础上减去 12 元后再打 0.8 折
答案:
C
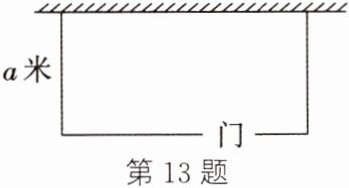
13. (易错题)(2025·绍兴新昌期末)如图是一面墙与篱笆围成的长方形园子,园子的宽为$a$米,篱笆的总长度为$b$米,门的宽度为 1 米,则园子的长是 ______ 米(用含$a$,$b$的代数式表示).

$(b-2a+1)$
答案:
$(b-2a+1)$ [易错分析]本题易忽视门的宽度为1米,导致出现错误答案$(b-2a)$;也会出现用篱笆的总长度先减去门的宽度,导致出现错误答案$(b-2a-1)$。
14. (教材 P104 作业题第 5 题变式)12 头大象 1 天的食品可供 1000 只老鼠吃 600 天. 假定每头大象的食量都相等,每只老鼠的食量也相等,那么$t$头大象 1 天的食品可供 100 只老鼠吃 ______ 天.
[答案]:
[答案]:
500t
答案:
500t
15. 如图,用棋子按规律摆出下列一组图形,据此规律,第 5 个图形有

17
枚棋子;第$n$($n$为正整数)个图形有 $(3n+2)$
枚棋子(用含$n$的代数式表示).
答案:
17 $(3n+2)$
16. 甲、乙两地之间的距离为$s\ \text{km}$,有两人分别骑自行车与摩托车从甲、乙两地同时出发,相向而行. 已知自行车的速度是$a\ \text{km/h}$,摩托车的速度是$b\ \text{km/h}$,则$t\ \text{h}$后,两人相距多少千米?
答案:
两人相距$(s-at-bt)$km或$(at+bt-s)$km
17. 为了促销一件定价为$m$元的商品,甲超市连续两次降价 20%;乙超市一次性降价 40%;丙超市第一次降价 30%,第二次降价 10%. 若顾客要购买这种商品,则去哪家超市最合算?
答案:
甲超市:$(1-20\%)^{2}m=0.64m$(元);乙超市:$(1-40\%)m=0.6m$(元);丙超市:$(1-30\%)(1-10\%)m=0.63m$(元).因为$0.64m>0.63m>0.6m$,所以去乙超市最合算
查看更多完整答案,请扫码查看


