《2025年暑假作业假期园地七年级语文数学英语合订本中原农民出版社》

12. 求下列各式中$x$的值.
(1)$x^{2}-144=0$; $x=\pm12$
(2)$(x-1)^{2}-2\frac {1}{4}=0$; $x=\frac{5}{2}$或$x=-\frac{1}{2}$
(3)$(2x-1)^{3}-216=0$; $x=\frac{7}{2}$
(4)$\frac {1}{2}(x+2)^{2}=\sqrt [3]{8}$. $x=0$或$x=-4$

答案： 【解析】：
1. 对于方程$x^{2}-144 = 0$，移项可得$x^{2}=144$，根据平方根的定义，一个正数有两个平方根，且互为相反数，所以$x=\pm\sqrt{144}=\pm12$。
2. 对于方程$(x - 1)^{2}-2\frac{1}{4}=0$，先将$2\frac{1}{4}$转化为$\frac{9}{4}$，则方程变为$(x - 1)^{2}=\frac{9}{4}$，根据平方根的定义，$x - 1=\pm\sqrt{\frac{9}{4}}=\pm\frac{3}{2}$。当$x - 1=\frac{3}{2}$时，$x=\frac{3}{2}+1=\frac{5}{2}$；当$x - 1=-\frac{3}{2}$时，$x=-\frac{3}{2}+1=-\frac{1}{2}$。
3. 对于方程$(2x - 1)^{3}-216 = 0$，移项可得$(2x - 1)^{3}=216$，根据立方根的定义，一个数的立方根只有一个，所以$2x - 1=\sqrt[3]{216}=6$，移项可得$2x=6 + 1=7$，解得$x=\frac{7}{2}$。
4. 对于方程$\frac{1}{2}(x + 2)^{2}=\sqrt[3]{8}$，先计算$\sqrt[3]{8}=2$，则方程变为$\frac{1}{2}(x + 2)^{2}=2$，两边同时乘以$2$得$(x + 2)^{2}=4$，根据平方根的定义，$x + 2=\pm\sqrt{4}=\pm2$。当$x + 2=2$时，$x=2-2 = 0$；当$x + 2=-2$时，$x=-2-2=-4$。
【答案】：1.$x=\pm12$ 2.$x=\frac{5}{2}$或$x=-\frac{1}{2}$ 3.$x=\frac{7}{2}$ 4.$x=0$或$x=-4$

13. 如图所示,在长方形$ABCD$中,$A(-4,1)$,$B(0,1)$,$C(0,3)$.
(1)求点$D$的坐标($(-4,3)$);
(2)求$S_{长方形ABCD}$($8$).

答案： 【解析】：
(1) 因为四边形$ABCD$是长方形，所以$AD = BC$，$AB = CD$，且$AD\perp AB$，$AB$在$x$轴方向，$AD$在$y$轴方向。
已知$A(-4,1)$，$B(0,1)$，$C(0,3)$，$AB$的长度为$\vert - 4-0\vert=4$，$BC$的长度为$\vert3 - 1\vert = 2$。
$D$点横坐标与$A$点横坐标相同，$D$点纵坐标与$C$点纵坐标相同，所以点$D$的坐标为$(-4,3)$。
(2) 根据长方形面积公式$S = 长\times宽$，由$A(-4,1)$，$B(0,1)$可得$AB$的长度$\vert - 4-0\vert=4$，由$B(0,1)$，$C(0,3)$可得$BC$的长度$\vert3 - 1\vert = 2$。
所以$S_{长方形ABCD}=AB\times BC=4\times2 = 8$。
【答案】：
(1)$(-4,3)$
(2)$8$

14. 如图是某水泥厂2012~2015年的产量(单位:万吨)统计图.

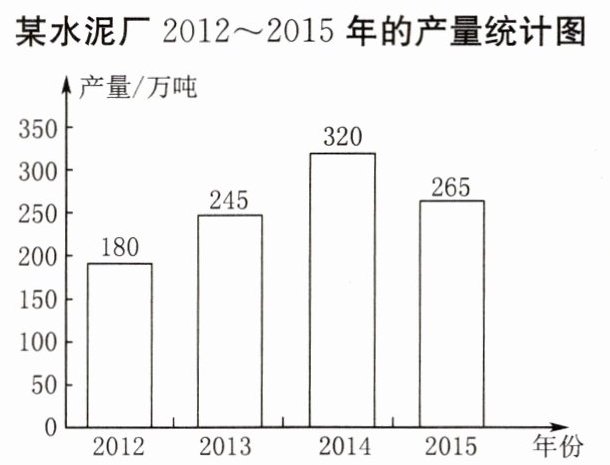
(1)2012~2015年水泥总产量是1010万吨?
(2)平均每年产量是252.5万吨?
(3)根据上图画出这四年产量的扇形图.
(4)根据这张统计图,试分析这个厂的生产情况,你预计2016年的产量是280万吨? 为什么?虽然2014-2015年产量下降，但整体生产有一定基础和波动规律，可能会有一定回升

答案： 【解析】：
(1)求$2012 - 2015$年水泥总产量，就是将这四年的产量相加，即$180 + 245 + 320 + 265$。
根据加法结合律$(a + b)+(c + d)=(a + d)+(b + c)$，可得$(180 + 320)+(245 + 265)=500 + 510 = 1010$（万吨）。
(2)求平均每年产量，根据“平均数$=$总数$\div$总份数”，总数是总产量$1010$万吨，总份数是$4$年，所以平均每年产量为$1010\div4 = 252.5$（万吨）。
(3)
先求各年占总产量的百分比：
$2012$年：$180\div1010\times100\%\approx17.8\%$，对应的扇形圆心角为$360^{\circ}\times17.8\%\approx64.1^{\circ}$。
$2013$年：$245\div1010\times100\%\approx24.3\%$，对应的扇形圆心角为$360^{\circ}\times24.3\%\approx87.5^{\circ}$。
$2014$年：$320\div1010\times100\%\approx31.7\%$，对应的扇形圆心角为$360^{\circ}\times31.7\%\approx114.1^{\circ}$。
$2015$年：$265\div1010\times100\%\approx26.2\%$，对应的扇形圆心角为$360^{\circ}\times26.2\%\approx94.3^{\circ}$。
然后根据以上数据画出扇形统计图（略，以实际测量绘制为准）。
(4)从统计图可以看出，$2012 - 2014$年产量呈上升趋势，$2014 - 2015$年产量下降。预计$2016$年产量（答案不唯一，合理即可），比如预计$2016$年产量为$280$万吨。原因是虽然$2014 - 2015$年产量下降，但整体生产有一定基础和波动规律，可能会有一定回升（具体分析结合实际情况，只要阐述合理即可）。
【答案】：
(1)$1010$万吨。
(2)$252.5$万吨。
(3)略（按上述计算角度绘制扇形图）。
(4)示例：预计$2016$年产量为$280$万吨。原因：虽然$2014 - 2015$年产量下降，但整体生产有一定基础和波动规律，可能会有一定回升（答案不唯一，合理即可）。