2025年暑假作业假期园地七年级语文数学英语合订本中原农民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业假期园地七年级语文数学英语合订本中原农民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 下列无理数中,在 - 2 与 1 之间的是(
A. $-\sqrt{5}$
B. $-\sqrt{3}$
C. $\sqrt{3}$
D. $\sqrt{5}$
B
)A. $-\sqrt{5}$
B. $-\sqrt{3}$
C. $\sqrt{3}$
D. $\sqrt{5}$
答案:
B
2. 已知实数 x,y 满足$\sqrt{x - 1}+|y + 3| = 0$,则.$x + y$的值为(
A. - 2
B. 2
C. 4
D. - 4
A
)A. - 2
B. 2
C. 4
D. - 4
答案:
A
3. 已知$Q(2x + 4,x^{2}-1)$在 y 轴上,则点 Q 的坐标为(
A. $(0,4)$
B. $(4,0)$
C. $(0,3)$
D. $(3,0)$
C
)A. $(0,4)$
B. $(4,0)$
C. $(0,3)$
D. $(3,0)$
答案:
C
4. 如图所示,已知$AC// BD,∠CAE = 30^{\circ},∠DBE = 45^{\circ}$,则$∠AEB$(小于$180^{\circ}$)等于(
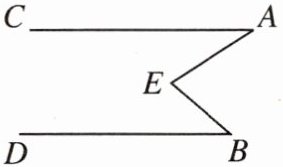
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$
D
)
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$
答案:
D
5. 如图所示,在平面直角坐标系中,$A(1,1),B(-1,1),C(-1,-2),D(1,-2)$. 把一条长为 2014 个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A 处,并按$A→B→C→D→A→\cdots$的规律紧绕在四边形 ABCD 的边上,则细线另一端所在位置的点的坐标是(
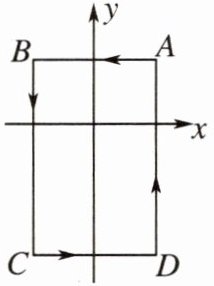
A. $(1,-1)$
B. $(-1,1)$
C. $(-1,-2)$
D. $(-1,-1)$
D
)
A. $(1,-1)$
B. $(-1,1)$
C. $(-1,-2)$
D. $(-1,-1)$
答案:
D
6. 学校的篮球数比足球数的 2 倍少 3 个,篮球数与足球数的比为$3:2$,则学校有篮球、足球共
15
个.
答案:
15
7. $\sqrt{81}$的算术平方根为 a,$\sqrt[3]{b}=2$,则$a - b=$
$-5$
.
答案:
$-5$
8. 如图,将正方形的一角折叠,折痕为 AE,$∠BAD$比$∠BAE$大$48^{\circ}$. 设$∠BAD$和$∠BAE$的度数分别为$x^{\circ}$和$y^{\circ}$,依题意可列方程为
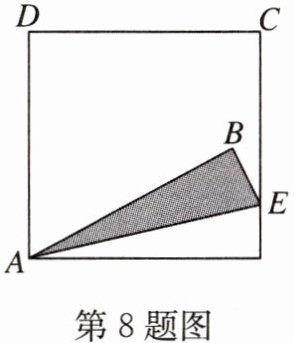
$\begin{cases}x - y = 48\\x + 2y = 90\end{cases}$
.
答案:
$\begin{cases}x - y = 48\\x + 2y = 90\end{cases}$
9. 如图,$AB// CD,∠BAE = 120^{\circ},∠DCE = 30^{\circ}$,则$∠AEC=$
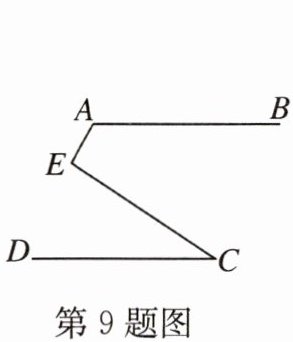
$90^{\circ}$
.
答案:
$90^{\circ}$
10. 解方程组:$\begin{cases}3x - 2y = - 1,①\\x + 3y = 7.②\end{cases}$
$\begin{cases}x = 1 \\ y = 2 \end{cases}$
答案:
【解析】:本题可使用消元法来解方程组。
- **步骤一:消去$x$,求出$y$的值**
为了消去$x$,可将方程②两边同时乘以$3$,得到$3x + 9y = 21$ ③。
用方程③减去方程①,可消去$x$,即$(3x + 9y)-(3x - 2y)=21-(-1)$,去括号得$3x + 9y - 3x + 2y = 21 + 1$,合并同类项得$11y = 22$,两边同时除以$11$,解得$y = 2$。
- **步骤二:将$y$的值代入方程②,求出$x$的值**
把$y = 2$代入方程②$x + 3y = 7$中,得到$x + 3×2 = 7$,即$x + 6 = 7$,两边同时减去$6$,解得$x = 1$。
【答案】:$\begin{cases}x = 1 \\ y = 2 \end{cases}$
- **步骤一:消去$x$,求出$y$的值**
为了消去$x$,可将方程②两边同时乘以$3$,得到$3x + 9y = 21$ ③。
用方程③减去方程①,可消去$x$,即$(3x + 9y)-(3x - 2y)=21-(-1)$,去括号得$3x + 9y - 3x + 2y = 21 + 1$,合并同类项得$11y = 22$,两边同时除以$11$,解得$y = 2$。
- **步骤二:将$y$的值代入方程②,求出$x$的值**
把$y = 2$代入方程②$x + 3y = 7$中,得到$x + 3×2 = 7$,即$x + 6 = 7$,两边同时减去$6$,解得$x = 1$。
【答案】:$\begin{cases}x = 1 \\ y = 2 \end{cases}$
11. 为了鼓励居民节约用水,某地规定用水收费标准如下:若每户每月的用水量不超过 20 方,水费为 x 元/方;若超过 20 方,不超过部分仍为 x 元/方,超过部分为 y 元/方. 已知某用户四月份用水 15 方,交水费 30 元,五月份用水 30 方,交水费 70 元.
(1)求 x,y 的值;
(2)若估计该用户六月份的水费支出不少于 64 元,但不超过 91 元. 求该用户六月份的用水量 w 的取值范围.
(1)求 x,y 的值;
(2)若估计该用户六月份的水费支出不少于 64 元,但不超过 91 元. 求该用户六月份的用水量 w 的取值范围.
答案:
【解析】:
1. 首先求$x$,$y$的值:
已知某用户四月份用水$15$方,$15\lt20$,根据“若每户每月的用水量不超过$20$方,水费为$x$元/方”,由四月份交水费$30$元,可得方程$15x = 30$,解得$x=\frac{30}{15}=2$。
又已知五月份用水$30$方,$30\gt20$,根据收费标准,不超过$20$方的部分水费为$20x$元,超过$20$方部分的水费为$(30 - 20)y$元,五月份交水费$70$元,则可列方程$20x+(30 - 20)y = 70$。
把$x = 2$代入$20x+(30 - 20)y = 70$中,得到$20\times2 + 10y=70$,即$40+10y = 70$,移项可得$10y=70 - 40$,$10y = 30$,解得$y = 3$。
2. 然后求该用户六月份用水量$w$的取值范围:
当$w\leqslant20$时,水费最多为$20\times2 = 40$元,而$64\gt40$,所以$w\gt20$。
当$w\gt20$时,水费为$20\times2+(w - 20)\times3$,化简可得$40+3w - 60=3w - 20$。
因为该用户六月份的水费支出不少于$64$元,但不超过$91$元,所以可得不等式组$\begin{cases}3w - 20\geqslant64\\3w - 20\leqslant91\end{cases}$。
解不等式$3w - 20\geqslant64$,移项得$3w\geqslant64 + 20$,$3w\geqslant84$,解得$w\geqslant28$。
解不等式$3w - 20\leqslant91$,移项得$3w\leqslant91+20$,$3w\leqslant111$,解得$w\leqslant37$。
【答案】:
(1)$x = 2$,$y = 3$;
(2)$28\leqslant w\leqslant37$
1. 首先求$x$,$y$的值:
已知某用户四月份用水$15$方,$15\lt20$,根据“若每户每月的用水量不超过$20$方,水费为$x$元/方”,由四月份交水费$30$元,可得方程$15x = 30$,解得$x=\frac{30}{15}=2$。
又已知五月份用水$30$方,$30\gt20$,根据收费标准,不超过$20$方的部分水费为$20x$元,超过$20$方部分的水费为$(30 - 20)y$元,五月份交水费$70$元,则可列方程$20x+(30 - 20)y = 70$。
把$x = 2$代入$20x+(30 - 20)y = 70$中,得到$20\times2 + 10y=70$,即$40+10y = 70$,移项可得$10y=70 - 40$,$10y = 30$,解得$y = 3$。
2. 然后求该用户六月份用水量$w$的取值范围:
当$w\leqslant20$时,水费最多为$20\times2 = 40$元,而$64\gt40$,所以$w\gt20$。
当$w\gt20$时,水费为$20\times2+(w - 20)\times3$,化简可得$40+3w - 60=3w - 20$。
因为该用户六月份的水费支出不少于$64$元,但不超过$91$元,所以可得不等式组$\begin{cases}3w - 20\geqslant64\\3w - 20\leqslant91\end{cases}$。
解不等式$3w - 20\geqslant64$,移项得$3w\geqslant64 + 20$,$3w\geqslant84$,解得$w\geqslant28$。
解不等式$3w - 20\leqslant91$,移项得$3w\leqslant91+20$,$3w\leqslant111$,解得$w\leqslant37$。
【答案】:
(1)$x = 2$,$y = 3$;
(2)$28\leqslant w\leqslant37$
12. 为了了解通话时长(通话时长指每次通话时间)的分布情况,小强收集了他家 1 000 个通话时长数据,这些数据均不超过 18 min. 他随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完整的频数分布直方图(如图所示).

根据图、表提供的信息,解答下面的问题:
(1)$a =$
(2)求样本中通话时长不超过 9 min 的频率;
(3)请估计小强家这 1 000 次通话中,通话时长超过 15 min 的次数.
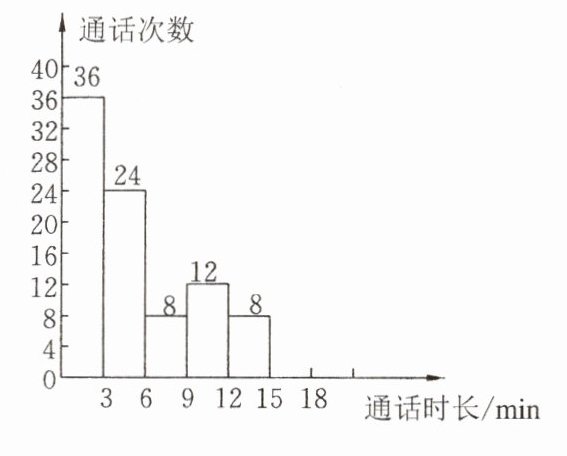

根据图、表提供的信息,解答下面的问题:
(1)$a =$
24
,样本容量是100
;(2)求样本中通话时长不超过 9 min 的频率;
(3)请估计小强家这 1 000 次通话中,通话时长超过 15 min 的次数.

答案:
【解析】:
1. 首先求$a$的值和样本容量:
由频数分布直方图可知,$3\lt x\leq6$这一组对应的频数$a = 24$。
样本容量是所有频数之和,即$36 + 24+8 + 12+8 + 12=100$。
2. 然后求样本中通话时长不超过$9min$的频率:
通话时长不超过$9min$的频数为$36 + 24+8=68$。
根据频率$=\frac{频数}{样本容量}$,可得频率为$\frac{68}{100}=0.68$。
3. 最后估计小强家这$1000$次通话中,通话时长超过$15min$的次数:
样本中通话时长超过$15min$的频率为$\frac{12}{100}=0.12$。
用样本估计总体,所以$1000$次通话中,通话时长超过$15min$的次数约为$1000\times0.12 = 120$次。
【答案】:1. $24$,$100$ 2. $0.68$ 3. $120$
1. 首先求$a$的值和样本容量:
由频数分布直方图可知,$3\lt x\leq6$这一组对应的频数$a = 24$。
样本容量是所有频数之和,即$36 + 24+8 + 12+8 + 12=100$。
2. 然后求样本中通话时长不超过$9min$的频率:
通话时长不超过$9min$的频数为$36 + 24+8=68$。
根据频率$=\frac{频数}{样本容量}$,可得频率为$\frac{68}{100}=0.68$。
3. 最后估计小强家这$1000$次通话中,通话时长超过$15min$的次数:
样本中通话时长超过$15min$的频率为$\frac{12}{100}=0.12$。
用样本估计总体,所以$1000$次通话中,通话时长超过$15min$的次数约为$1000\times0.12 = 120$次。
【答案】:1. $24$,$100$ 2. $0.68$ 3. $120$
查看更多完整答案,请扫码查看


