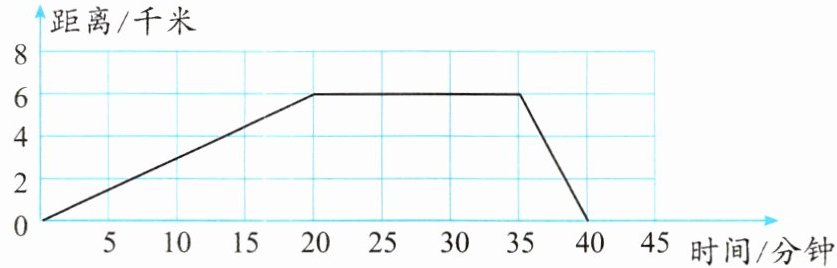
3.李叔叔下午1:40骑自行车从家出发,去离家6千米远的图书馆借书,借了书后因为自行车坏了,乘出租车回家。下图表示在这段时间里李叔叔离家的距离的变化情况。
(1)李叔叔在图书馆里待了多长时间?回到家是什么时刻(用24时计时法表示)?
(2)李叔叔去图书馆平均每分钟行多少千米?

(1)李叔叔在图书馆里待了多长时间?回到家是什么时刻(用24时计时法表示)?
(2)李叔叔去图书馆平均每分钟行多少千米?
答案:
解析:本题主要考查了时间与距离的关系以及平均速度的计算。需要从图表中获取关键信息,并结合时间换算和平均速度公式来进行计算。
(1)首先,需要找到李叔叔在图书馆停留的时间段。
从图表中可以看出,在20分钟到35分钟这段时间内,李叔叔离家的距离没有变化,保持在6千米,这说明他在这段时间内在图书馆。
因此,李叔叔在图书馆待的时间为:$35 - 20 = 15$(分钟)。
接下来,需要确定李叔叔回到家的时刻。
从图表中可以看出,李叔叔在40分钟时开始回家,假设他回家所用的时间和去图书馆的时间相同,即20分钟。
所以,他应该在$40+20=60$(分钟),即下午2点40分的时候到家。用24时计时法表示为14:40。
所以,李叔叔在图书馆待了15分钟,他回到家的时刻为14:40。
(2)为了计算李叔叔去图书馆的平均速度,需要知道他去图书馆所用的时间和距离。
从图表中可以看出,李叔叔去图书馆所用的时间为20分钟,距离为6千米。
将20分钟转换为小时,即 $\frac{20}{60} = \frac{1}{3} $(小时)。
使用平均速度的公式:$平均速度= \frac{距离}{时间} $。
代入已知数值:$平均速度 = \frac{6}{\frac{1}{3}} = 6 × 3 = 0.3×60=18$(千米/小时),
18千米/小时=0.3千米/分钟。
所以,李叔叔去图书馆平均每分钟行0.3千米。
(1)首先,需要找到李叔叔在图书馆停留的时间段。
从图表中可以看出,在20分钟到35分钟这段时间内,李叔叔离家的距离没有变化,保持在6千米,这说明他在这段时间内在图书馆。
因此,李叔叔在图书馆待的时间为:$35 - 20 = 15$(分钟)。
接下来,需要确定李叔叔回到家的时刻。
从图表中可以看出,李叔叔在40分钟时开始回家,假设他回家所用的时间和去图书馆的时间相同,即20分钟。
所以,他应该在$40+20=60$(分钟),即下午2点40分的时候到家。用24时计时法表示为14:40。
所以,李叔叔在图书馆待了15分钟,他回到家的时刻为14:40。
(2)为了计算李叔叔去图书馆的平均速度,需要知道他去图书馆所用的时间和距离。
从图表中可以看出,李叔叔去图书馆所用的时间为20分钟,距离为6千米。
将20分钟转换为小时,即 $\frac{20}{60} = \frac{1}{3} $(小时)。
使用平均速度的公式:$平均速度= \frac{距离}{时间} $。
代入已知数值:$平均速度 = \frac{6}{\frac{1}{3}} = 6 × 3 = 0.3×60=18$(千米/小时),
18千米/小时=0.3千米/分钟。
所以,李叔叔去图书馆平均每分钟行0.3千米。
如何找到合适的分数
亮亮请教明明和贝贝一个数学问题:写出一个大于$\frac{1}{6}且小于\frac{1}{5}$的分数。
明明说:“你先将$\frac{1}{6}和\frac{1}{5}$通分,即这个分数在$\frac{5}{30}和\frac{6}{30}$之间。在$\frac{5}{30}和\frac{6}{30}$之间还不能很快地找到这个分数,我们可以利用分数的基本性质,将$\frac{5}{30}和\frac{6}{30}$的分子和分母同时扩大到原来的2倍,即$\frac{10}{60}<□<\frac{12}{60}$,你看能找出符合条件的分数吗?”
亮亮高兴地说:“分数$\frac{11}{60}$符合条件。我懂了,我可以继续将$\frac{5}{30}和\frac{6}{30}$的分子和分母同时扩大到原来的3倍得到$\frac{15}{90}<□<\frac{18}{90}$,就有$\frac{16}{90}$(即$\frac{8}{45}$)、$\frac{17}{90}$符合条件。如果需要找更多的分数,那么我还可以继续扩大。”
贝贝说:“还可以先将分数化成小数,即这个分数在$0.1666…和0.2$之间,就可以找到$0.17$、$0.18$、$0.19$等小数符合条件,然后再将这些符合条件的小数化成分数,能约分的约成最简分数。可见,大于$\frac{1}{6}且小于\frac{1}{5}的分数有\frac{17}{100}$、$\frac{18}{100}$(即$\frac{9}{50}$)、$\frac{19}{100}$等。”
亮亮请教明明和贝贝一个数学问题:写出一个大于$\frac{1}{6}且小于\frac{1}{5}$的分数。
明明说:“你先将$\frac{1}{6}和\frac{1}{5}$通分,即这个分数在$\frac{5}{30}和\frac{6}{30}$之间。在$\frac{5}{30}和\frac{6}{30}$之间还不能很快地找到这个分数,我们可以利用分数的基本性质,将$\frac{5}{30}和\frac{6}{30}$的分子和分母同时扩大到原来的2倍,即$\frac{10}{60}<□<\frac{12}{60}$,你看能找出符合条件的分数吗?”
亮亮高兴地说:“分数$\frac{11}{60}$符合条件。我懂了,我可以继续将$\frac{5}{30}和\frac{6}{30}$的分子和分母同时扩大到原来的3倍得到$\frac{15}{90}<□<\frac{18}{90}$,就有$\frac{16}{90}$(即$\frac{8}{45}$)、$\frac{17}{90}$符合条件。如果需要找更多的分数,那么我还可以继续扩大。”
贝贝说:“还可以先将分数化成小数,即这个分数在$0.1666…和0.2$之间,就可以找到$0.17$、$0.18$、$0.19$等小数符合条件,然后再将这些符合条件的小数化成分数,能约分的约成最简分数。可见,大于$\frac{1}{6}且小于\frac{1}{5}的分数有\frac{17}{100}$、$\frac{18}{100}$(即$\frac{9}{50}$)、$\frac{19}{100}$等。”
答案:
解析:本题主要考查分数比较大小以及通分。
题目要求找到一个大于$\frac{1}{6}$且小于$\frac{1}{5}$的分数。
首先,将两个分数通分,
因为$6$和$5$的最小公倍数是$30$,
所以$\frac{1}{6}=\frac{1 × 5}{6 × 5}=\frac{5}{30}$,$\frac{1}{5}=\frac{1 × 6}{5 × 6}=\frac{6}{30}$,
但因为在$\frac{5}{30}$和$\frac{6}{30}$之间没有明显的分数,
所以需要将这两个分数的分子和分母同时扩大相同的倍数,
这里选择扩大$2$倍,
得到:
$\frac{5 × 2}{30 × 2}=\frac{10}{60}$,
$\frac{6 × 2}{30 × 2}=\frac{12}{60}$,
在$\frac{10}{60}$和$\frac{12}{60}$之间,可以找到分数$\frac{11}{60}$,
它满足大于$\frac{1}{6}$且小于$\frac{1}{5}$的条件,
为了找到更多满足条件的分数,可以继续将分子和分母扩大相同的倍数,
如扩大$3$倍,得到:
$\frac{5 × 3}{30 × 3}=\frac{15}{90}$,
$\frac{6 × 3}{30 × 3}=\frac{18}{90}$,
在$\frac{15}{90}$和$\frac{18}{90}$之间,可以找到分数$\frac{16}{90}$(化简为$\frac{8}{45}$)和$\frac{17}{90}$,
它们也满足大于$\frac{1}{6}$且小于$\frac{1}{5}$的条件,
另外,还可以将分数化为小数来寻找满足条件的分数,
即$\frac{1}{6} \approx 0.1666\ldots$,$\frac{1}{5} = 0.2$,
在$0.1666\ldots$和$0.2$之间,可以找到小数$0.17$、$0.18$、$0.19$等,
然后将这些小数化成分数,能约分的约成最简分数,
如$0.17 = \frac{17}{100}$,$0.18 = \frac{18}{100} = \frac{9}{50}$,$0.19 = \frac{19}{100}$,
它们都满足大于$\frac{1}{6}$且小于$\frac{1}{5}$的条件。
答案为:通过通分和扩大分子分母的方法,或者将分数化为小数的方法,可以找到大于$\frac{1}{6}$且小于$\frac{1}{5}$的分数,如$\frac{11}{60}$,$\frac{8}{45}$,$\frac{17}{100}$,$\frac{9}{50}$,$\frac{19}{100}$等。
题目要求找到一个大于$\frac{1}{6}$且小于$\frac{1}{5}$的分数。
首先,将两个分数通分,
因为$6$和$5$的最小公倍数是$30$,
所以$\frac{1}{6}=\frac{1 × 5}{6 × 5}=\frac{5}{30}$,$\frac{1}{5}=\frac{1 × 6}{5 × 6}=\frac{6}{30}$,
但因为在$\frac{5}{30}$和$\frac{6}{30}$之间没有明显的分数,
所以需要将这两个分数的分子和分母同时扩大相同的倍数,
这里选择扩大$2$倍,
得到:
$\frac{5 × 2}{30 × 2}=\frac{10}{60}$,
$\frac{6 × 2}{30 × 2}=\frac{12}{60}$,
在$\frac{10}{60}$和$\frac{12}{60}$之间,可以找到分数$\frac{11}{60}$,
它满足大于$\frac{1}{6}$且小于$\frac{1}{5}$的条件,
为了找到更多满足条件的分数,可以继续将分子和分母扩大相同的倍数,
如扩大$3$倍,得到:
$\frac{5 × 3}{30 × 3}=\frac{15}{90}$,
$\frac{6 × 3}{30 × 3}=\frac{18}{90}$,
在$\frac{15}{90}$和$\frac{18}{90}$之间,可以找到分数$\frac{16}{90}$(化简为$\frac{8}{45}$)和$\frac{17}{90}$,
它们也满足大于$\frac{1}{6}$且小于$\frac{1}{5}$的条件,
另外,还可以将分数化为小数来寻找满足条件的分数,
即$\frac{1}{6} \approx 0.1666\ldots$,$\frac{1}{5} = 0.2$,
在$0.1666\ldots$和$0.2$之间,可以找到小数$0.17$、$0.18$、$0.19$等,
然后将这些小数化成分数,能约分的约成最简分数,
如$0.17 = \frac{17}{100}$,$0.18 = \frac{18}{100} = \frac{9}{50}$,$0.19 = \frac{19}{100}$,
它们都满足大于$\frac{1}{6}$且小于$\frac{1}{5}$的条件。
答案为:通过通分和扩大分子分母的方法,或者将分数化为小数的方法,可以找到大于$\frac{1}{6}$且小于$\frac{1}{5}$的分数,如$\frac{11}{60}$,$\frac{8}{45}$,$\frac{17}{100}$,$\frac{9}{50}$,$\frac{19}{100}$等。
查看更多完整答案,请扫码查看


