《2025年暑假作业本大象出版社八年级物理通用版》

18. 如图6-18所示,一辆货车从山底A匀速开到山顶B。货车重为$5.0×10^{4}N$,发动机的功率为50kW且保持不变,山坡AB长2000m、高h为300m,牵引力保持$2.5×10^{4}N$不变,不计空气阻力。求：

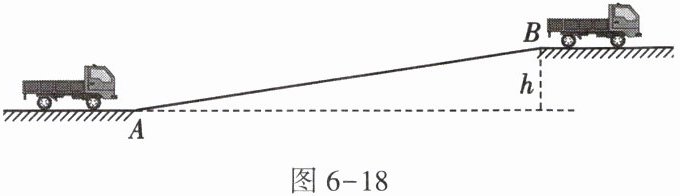
(1)货车从山底开到山顶所做的有用功；
(2)山坡的机械效率；
(3)货车在山坡上行驶时所受的摩擦力。

答案：
(1) 由题意可知，货车从山底开到山顶所做的有用功
$W_{有用} = Gh = 5.0×10^{4}N×300m = 1.5×10^{7}J$。
(2) 由 $W = Fs$ 可知，汽车从山底开到山顶所做的总功
$W_{总} = Fs = 2.5×10^{4}N×2000m = 5×10^{7}J$，
由 $\eta = \frac{W_{有用}}{W_{总}}$ 可知，山坡的机械效率
$\eta = \frac{W_{有用}}{W_{总}} = \frac{1.5×10^{7}J}{5×10^{7}J} = 30\%$。
(3) 由题意可知，额外功
$W_{额外} = W_{总} - W_{有用} = 5×10^{7}J - 1.5×10^{7}J = 3.5×10^{7}J$，
由 $W_{额外} = fs$ 可知，汽车在山坡上行驶时的摩擦力
$f = \frac{W_{额外}}{s} = \frac{3.5×10^{7}J}{2000m} = 1.75×10^{4}N$。

19. 我国民俗活动丰富多彩,在立夏时节,有的地方会用杆秤测量孩子的质量,冀求孩子健康成长,俗称“立夏秤人”。如图6-19甲所示,若孩子和篮子的总质量为10kg,调整秤砣的位置,使秤杆处于水平平衡状态(忽略绳重和杆重),如图6-19乙所示,此时OA= 3cm,OB= 10cm。下列说法错误的是()

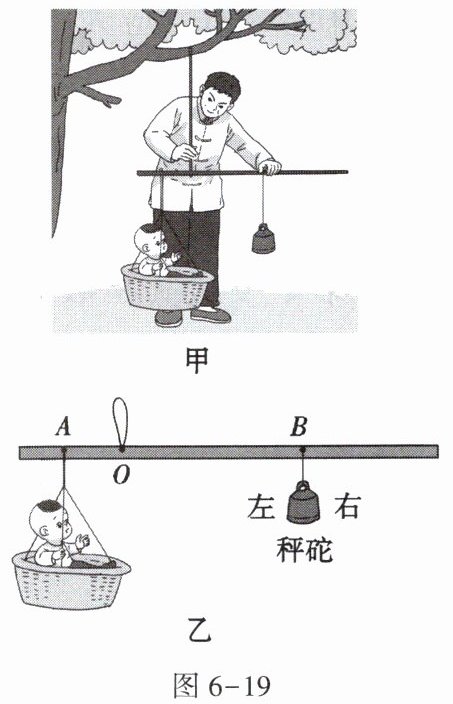
A. 该秤砣的质量为3kg
B. 若秤砣被碰掉一块,则所称质量偏大
C. 要使该杆秤的测量范围变大,应该换用质量更小的秤砣
D. 若换称质量较小的孩子,当秤杆水平平衡时,秤砣的悬挂点在B点左侧

答案： C