《2025年暑假作业本大象出版社八年级物理通用版》

17. 浮式起重机又称起重船,它可以利用船体提供的浮力和船上的起重系统来完成起吊作业。如图4-13甲是某起重船,图4-13乙是它的简化示意图。OB是起重臂,向上提升重物时,起重臂OB保持静止,通过固定在B点的绞车(图中未画出)回收钢缆,将重物吊起。(不计起重臂、绞车和钢缆的重力,不计摩擦,$\rho_{海水}= 1.0×10^{3}kg/m^{3}$,g取10N/kg)

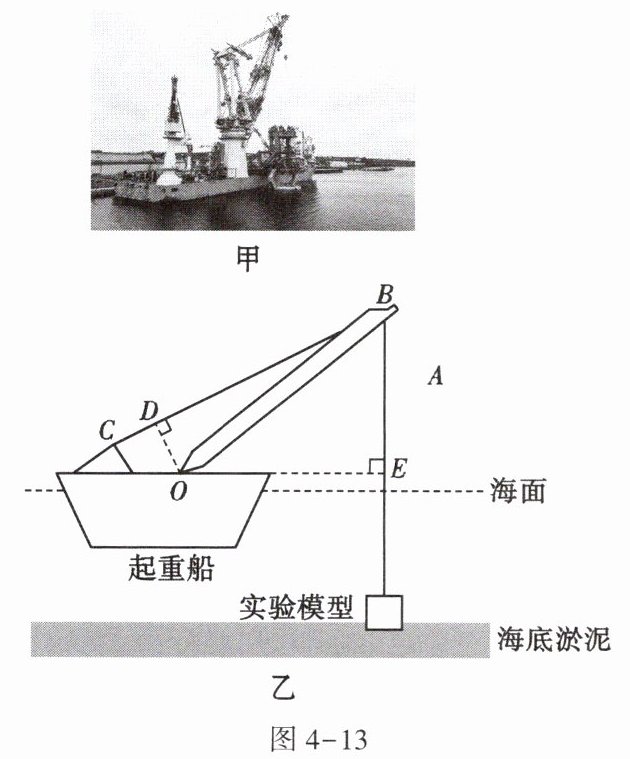
(1)如图4-13乙所示,某次模拟打捞作业时,密闭长方体实验模型底部嵌入海底淤泥中,顶部到海面的距离为100m,则海水对实验模型顶部的压强为多少？
(2)该实验模型的长为5m,宽为4m,高为5m,总质量为600t。起吊前,先向船舱中注入适量的水,再将钢缆紧紧地连接到绞车上。接着逐渐排出船舱中的水并保持吃水深度不变,当钢缆刚好能拉动实验模型时,停止排水。问：此时钢缆对实验模型的拉力为多少？
(3)为了使实验模型脱离淤泥,起重船至少需要向外排出多少立方米的海水？

答案：
(1) 密闭长方体实验模型顶部到海面的距离为 100 m，则海水对实验模型顶部的压强$p=\rho_{海水}gh=1.0\times10^{3}kg/m^{3}\times10N/kg\times100m=1.0\times10^{6}Pa$。
(2) 模型顶部的面积$S=5m\times4m=20m^{2}$，受到海水的压力$F=pS=1.0\times10^{6}Pa\times20m^{2}=2\times10^{7}N$；模型总质量$m=600t=6\times10^{5}kg$，则重力$G=mg=6\times10^{5}kg\times10N/kg=6\times10^{6}N$；当钢缆刚好能拉动模型时，海底淤泥对模型的支撑力为零，模型受力平衡，由于模型陷入海底淤泥中，所以不受浮力作用，即钢缆对模型的拉力$F_{拉}=F+G=2\times10^{7}N+6\times10^{6}N=2.6\times10^{7}N$。
(3) 由于起重船的船身稳定且吃水深度保持不变，则起重船受到浮力不变，则排出船舱中水的重力等于钢缆的拉力，所以$G_{排}=F_{拉}=2.6\times10^{7}N$，则$m_{排}=\frac{G_{排}}{g}=\frac{2.6\times10^{7}N}{10N/kg}=2.6\times10^{6}kg$；由密度公式可知，排开的海水的体积$V_{排}=\frac{m_{排}}{\rho_{海水}}=\frac{2.6\times10^{6}kg}{1.0\times10^{3}kg/m^{3}}=2.6\times10^{3}m^{3}$。