《2025年奔跑吧少年八年级数学上册浙教版》

23. (1)如图①,在$\triangle ABC$中,$AB = 5$,$AC = 7$,AD是BC边上的中线,延长AD至点E,使$DE = AD$,连结CE,把AB,AC,2AD集中在$\triangle ACE$中,利用三角形三边关系可得AD的取值范围。请写出AD的取值范围,并说明理由。
(2)如图②,在$\triangle ABC$中,AD是BC边上的中线,点E,F分别在AB,AC上,且$DE \perp DF$。求证：$BE + CF ＞ EF$。小艾同学受到(1)的启发,在解决(2)的问题时,延长ED至点H,使$DH = DE$…,请你帮她完成证明过程。

答案： $(1)$ 求$AD$的取值范围
- **步骤一：证明$\triangle ABD\cong\triangle ECD$
已知$AD$是$BC$边上的中线，则$BD = CD$，又因为$\angle ADB=\angle EDC$（对顶角相等），$DE = AD$。
根据$SAS$（边角边）判定定理，可得$\triangle ABD\cong\triangle ECD$。
- **步骤二：根据全等三角形性质得到边的关系
由$\triangle ABD\cong\triangle ECD$，根据全等三角形对应边相等，可得$AB = EC = 5$。
- **步骤三：利用三角形三边关系求$AD$的取值范围
在$\triangle ACE$中，根据三角形三边关系：两边之和大于第三边，两边之差小于第三边，即$AC - EC\lt AE\lt AC + EC$。
因为$AE=AD + DE = 2AD$，$AC = 7$，$EC = 5$，所以$7 - 5\lt 2AD\lt 7 + 5$，即$2\lt 2AD\lt 12$，两边同时除以$2$，得到$1\lt AD\lt 6$。
$(2)$ 证明$BE + CF\gt EF$
- **步骤一：证明$\triangle BDE\cong\triangle CDH$
延长$ED$至点$H$，使$DH = DE$，连接$CH$，$FH$。
因为$AD$是$BC$边上的中线，所以$BD = CD$，又$\angle BDE=\angle CDH$（对顶角相等）。
根据$SAS$（边角边）判定定理，可得$\triangle BDE\cong\triangle CDH$。
- **步骤二：根据全等三角形性质得到边的关系
由$\triangle BDE\cong\triangle CDH$，根据全等三角形对应边相等，可得$BE = CH$。
- **步骤三：证明$EF = FH$
因为$DE\perp DF$，$DE = DH$，所以$DF$是线段$EH$的垂直平分线（垂直平分线的定义：到线段两端距离相等的点在线段的垂直平分线上）。
根据垂直平分线的性质：线段垂直平分线上的点到线段两端的距离相等，可得$EF = FH$。
- **步骤四：利用三角形三边关系证明结论
在$\triangle CFH$中，根据三角形三边关系：两边之和大于第三边，即$CH + CF\gt FH$。
因为$BE = CH$，$EF = FH$，所以$BE + CF\gt EF$。
综上，$(1)$$\boldsymbol{1\lt AD\lt 6}$；$(2)$证明过程如上述步骤。

24. 在$\triangle ABC$中,点D在直线AB上,点E在平面内,点F在BC的延长线上,$\angle E = \angle BDC$,$AE = CD$,$\angle EAB + \angle DCF = 180^{\circ}$。
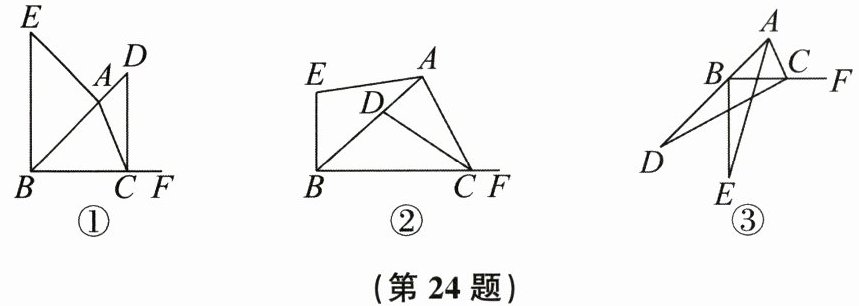
【问题解决】(1)如图①,若点D在BA的延长线上,求证：$AD + BC = BE$。
【类比探究】(2)如图②,若点D在线段AB上,请探究线段AD,BC与BE之间存在怎样的数量关系,并说明理由。
【拓展延伸】(3)如图③,若点D在线段AB的延长线上,请直接写出线段AD,BC与BE之间的数量关系：____AD - BC = BE。

答案：
(1)略
(2)$ BC - AD = BE $，理由略。
(3)$ AD - BC = BE $