2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23. 在平面直角坐标系中,对于点$P_{n}(x,y)$,若点$Q_{n}的坐标为(x+y,x-y)$,则称点$Q_{n}为点P_{n}$的“关联点”。例如,点$P_{0}(1,2)$,则点$Q_{0}(3,-1)是点P_{0}$的“关联点”。
(1)若点$P_{1}(3,2)$,点$Q_{1}是点P_{1}$的“关联点”,则点$Q_{1}$的坐标为
(2)若点$Q_{3}在y$轴上,点$Q_{3}是点P_{3}$的“关联点”,则点$P_{3}(x,y)中x,y$的关系为
(3)若点$Q_{4}是点P_{4}$的“关联点”,点$P_{4}$向右平移3个单位长度可与点$Q_{4}$重合,求点$P_{4}$的坐标。
(1)若点$P_{1}(3,2)$,点$Q_{1}是点P_{1}$的“关联点”,则点$Q_{1}$的坐标为
(5,1)
;若点$Q_{2}(0,4)$,点$Q_{2}是点P_{2}$的“关联点”,则点$P_{2}$的坐标为(-2,2)
。(2)若点$Q_{3}在y$轴上,点$Q_{3}是点P_{3}$的“关联点”,则点$P_{3}(x,y)中x,y$的关系为
x+y=0
。(3)若点$Q_{4}是点P_{4}$的“关联点”,点$P_{4}$向右平移3个单位长度可与点$Q_{4}$重合,求点$P_{4}$的坐标。
(6,3)
答案:
(1)$(5,1)$ $(-2,2)$
(2)$x+y=0$
(3)$(6,3)$。
(1)$(5,1)$ $(-2,2)$
(2)$x+y=0$
(3)$(6,3)$。
24. 如图,在以$O$为原点的平面直角坐标系中,点$A,B的坐标分别为(a,0),(a,b)$,点$C在y$轴上,且$BC// x$轴,$a,b满足|a-3|+(b-4)^{2}= 0$。点$P$从原点出发,以每秒2个单位长度的速度沿着$O-A-B-C-O$的路线运动(回到点$O$停止)。
(1)写出点$A,B,C$的坐标。
(2)当点$P$运动4秒时,求出点$P$的坐标。
(3)点$P运动t(t\neq0)$秒后,是否存在点$P到x轴的距离为\frac{1}{2}t$个单位长度的情况?若存在,求出点$P$的坐标;若不存在,请说明理由。
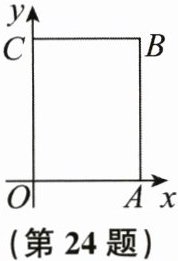
(1)写出点$A,B,C$的坐标。
(2)当点$P$运动4秒时,求出点$P$的坐标。
(3)点$P运动t(t\neq0)$秒后,是否存在点$P到x轴的距离为\frac{1}{2}t$个单位长度的情况?若存在,求出点$P$的坐标;若不存在,请说明理由。

答案:
(1)点$A(3,0)$,$B(3,4)$,$C(0,4)$。
(2)$(2,4)$。
(3)存在,点P的坐标为$(3,1)$或$(0,\frac{14}{5})$。
(1)点$A(3,0)$,$B(3,4)$,$C(0,4)$。
(2)$(2,4)$。
(3)存在,点P的坐标为$(3,1)$或$(0,\frac{14}{5})$。
查看更多完整答案,请扫码查看


