《2025年奔跑吧少年八年级数学上册浙教版》

11. “x的3倍与4的差不小于2”用不等式可表示为$ 3x - 4 \geq 2 $。

答案： $ 3x - 4 \geq 2 $

12. 命题“三角形的三个内角中至少有一个大于或等于$60^{\circ }$”是真命题。

答案： 真

13. 已知三角形的一个内角是$40^{\circ }$,则当此三角形的另外两个角中有一个角等于$ 100^{\circ} $或 $ 70^{\circ} $或 $ 40^{\circ} $时,这个三角形是等腰三角形。

答案： $ 100^{\circ} $或 $ 70^{\circ} $或 $ 40^{\circ} $

14. 如图,在$△ABC$中,BO平分$∠ABC$,CO平分$∠ACB$,过点O作$MN// BC$交AB于点M,交AC于点N。若$△ANM$的周长为15,$△ABC$的周长为24,则BC的值为____9。

答案： 9

15. 不等式组$\left\{\begin{array}{l} 3x＞2x-1,\\ 2x+3≤5\end{array}\right. 的整数解均满足不等式组\frac{a-6}{5}＜x≤a$,则a的取值范围是$ 1 \leq a ＜ 6 $。

答案： $ 1 \leq a ＜ 6 $

16. 如图,折叠等腰三角形纸片ABC,使点C落在边AB上的点F处,折痕为DE。
(1)已知$AB= AC,FD⊥BC$,则$∠AFE$的度数为$90^{\circ}$。
(2)在(1)的条件下,若$AF= 4,BF= 6$,则AE的值为$\frac{29}{5}$。

答案：
(1) $ 90^{\circ} $
(2) $ \frac{29}{5} $

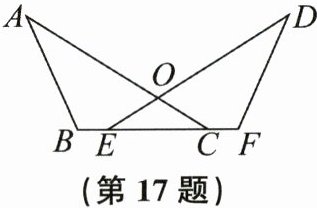
17. 如图,AC与DE相交于点O,且$OA= OD,∠ACB= ∠DEF$,点E,C在BF上,$BE= FC$。求证:$△ABC≌△DFE$。

答案： 【解析】：
- 因为$BE = FC$，根据等式的性质，在等式两边同时加上$EC$，可得$BE + EC = FC + EC$，即$BC = FE$。
- 在$\triangle AOC$和$\triangle DOE$中，$\left\{\begin{array}{l}∠AOC = ∠DOE\\OA = OD\\∠ACB = ∠DEF\end{array}\right.$，根据“$ASA$”（两角及其夹边对应相等的两个三角形全等）可证$\triangle AOC\cong\triangle DOE$，所以$AC = DE$。
- 在$\triangle ABC$和$\triangle DFE$中，$\left\{\begin{array}{l}AC = DE\\∠ACB = ∠DEF\\BC = FE\end{array}\right.$，根据“$SAS$”（两边及其夹角对应相等的两个三角形全等）可证$\triangle ABC\cong\triangle DFE$。
【答案】：
$\because BE = FC$，$\therefore BE + EC = FC + EC$，即$BC = FE$。
在$\triangle AOC$和$\triangle DOE$中，$\left\{\begin{array}{l}∠AOC = ∠DOE\\OA = OD\\∠ACB = ∠DEF\end{array}\right.$，$\therefore\triangle AOC\cong\triangle DOE(ASA)$，$\therefore AC = DE$。
在$\triangle ABC$和$\triangle DFE$中，$\left\{\begin{array}{l}AC = DE\\∠ACB = ∠DEF\\BC = FE\end{array}\right.$，$\therefore\triangle ABC\cong\triangle DFE(SAS)$。

18. 解不等式(组),并将解集表示在数轴上。
(1)$2x-5＜x-6$。
(2)$\left\{\begin{array}{l} x-1≥0,\\ x+8＞4x+2。\end{array}\right. $

答案：
(1) $ x ＜ -1 $，解集表示在数轴上略。
(2) $ 1 \leq x ＜ 2 $，解集表示在数轴上略。

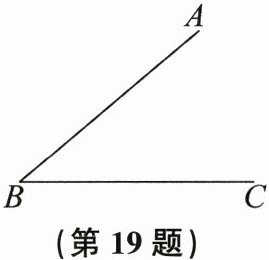
19. 随着知识的不断学习,小明发现了一种新的作角的平分线的方法。具体作法如下:
①在边AB上任取一点D,画$∠ADE$(点E在$∠ABC$的内部),使$∠ADE= ∠ABC$;
②在射线DE上截取$DF= DB$;
③画射线BF,射线BF即为$∠ABC$的平分线。
(1)请按照小明的作法,画出$∠ABC$的平分线。
(2)试说明射线BF是$∠ABC$的平分线的理由。

答案： 【解析】：
(1) 按照步骤：
①在边$AB$上任取一点$D$，用量角器画$\angle ADE$（点$E$在$\angle ABC$的内部），使$\angle ADE=\angle ABC$；
②用圆规在射线$DE$上截取$DF = DB$；
③连接$BF$，画出射线$BF$。
(2) 因为$\angle ADE=\angle ABC$，根据“同位角相等，两直线平行”，所以$DE// BC$。
由$DE// BC$，根据“两直线平行，内错角相等”，可得$\angle DFB=\angle FBC$。
又因为$DF = DB$，根据“等边对等角”，所以$\angle DBF=\angle DFB$。
通过等量代换，$\angle DBF=\angle FBC$，所以射线$BF$是$\angle ABC$的平分线。
【答案】：
(1) 按上述步骤画出$\angle ABC$的平分线$BF$（具体图形略，需学生根据步骤实际操作绘制）。
(2) 理由：因为$\angle ADE=\angle ABC$，所以$DE// BC$（同位角相等，两直线平行），则$\angle DFB=\angle FBC$（两直线平行，内错角相等），又$DF = DB$，所以$\angle DBF=\angle DFB$（等边对等角），故$\angle DBF=\angle FBC$，即射线$BF$是$\angle ABC$的平分线。