《2025年亮点激活提优天天练四年级数学下册北师大版》

1. 下面的三幅图，可以看作是密铺吗？为什么？

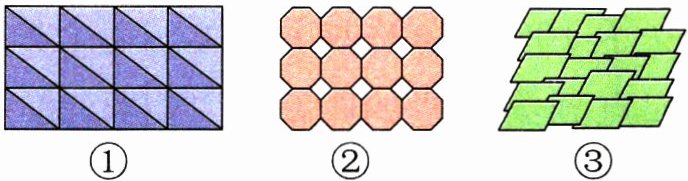
图( )是密铺图形。图②有空隙，图③有重叠，都( )(填“是”或“不是”)密铺。

答案： ①@@不是

2. 判一判。(对的画“√”，错的画“×”)
(1)只要图形之间没有空隙，就是密铺。( )
(2)所有的平面图形都能密铺。( )
(3)密铺时只能用一种图形。( )
(4)任意形状、大小相同的三角形都能密铺。( )

答案： ×
@@×
@@×
@@√

(1)下列正多边形中，不能单独用来密铺的是( )。
A.正六边形
B.正八边形
C.正方形
D.正三角形
(2)用几种不同边数的正多边形镶嵌，必须满足在一个顶点处的所有正多边形的一个内角的和为( )。
A.360°
B.300°
C.240°
D.180°
(3)下面的图形中，能单独密铺的有( )个。

A.2
B.3
C.4

答案： B
@@A
@@A

4. 用边长相同的正三角形和正方形两种平面图形是否能进行密铺？如果能，请画出草图，说明铺法；如果不能，请说明理由。

答案： 能，同一拼接点处有两个正方形和三个三角形。图略

5. 如果下面每个正方形都是由4个完全相同的图形密铺而成，你有哪些画法？请你画一画。

答案：

6. 用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案。

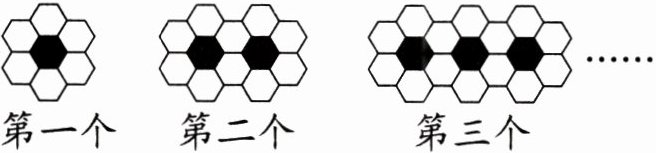
(1)第四个图案中有白色地砖( )块。
(2)第n个图案中有白色地砖( )块。

答案： 18@@4n + 2