第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 填一填。
(1)在一个三角形中,最大的角是 78°,这个三角形是( )三角形。
(2)一个三角形的两个内角分别是 95°和 27°,则另一个内角的度数是( )。
(3)把一个较大的三角形剪成两个不同的小三角形,剪出的两个小三角形内角和 ( ),它们的内角和都是( )。
(1)在一个三角形中,最大的角是 78°,这个三角形是( )三角形。
(2)一个三角形的两个内角分别是 95°和 27°,则另一个内角的度数是( )。
(3)把一个较大的三角形剪成两个不同的小三角形,剪出的两个小三角形内角和 ( ),它们的内角和都是( )。
答案:
锐角@@$58^{\circ}$@@相等@@$180^{\circ}$
2. 判一判。(对的画“√”,错的画“×”)
(1)一个三角形三个内角度数分别是 30°、80°和 60°。 ( )
(2)一个三角形中,最大的内角一定不能小于 60°。 ( )
(3)一个三角形的两个内角分别是 91°和 89°。 ( )
(4)一个三角形中,最小的锐角大于 45°,这个三角形是锐角三角形。 ( )
(1)一个三角形三个内角度数分别是 30°、80°和 60°。 ( )
(2)一个三角形中,最大的内角一定不能小于 60°。 ( )
(3)一个三角形的两个内角分别是 91°和 89°。 ( )
(4)一个三角形中,最小的锐角大于 45°,这个三角形是锐角三角形。 ( )
答案:
×@@√@@×@@√
3. 选一选。
(1)如果一个三角形中两个内角的和是 90°,那么这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
(2)锐角三角形 ABC 中,∠1 + ∠2 一定( )。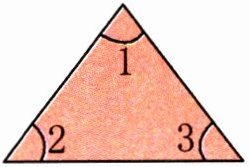
A.大于 90°
B.小于 90°
C.等于 90°
(3)等腰三角形一定有两个内角相等,而且这两个相等的内角一定是( )角。
A.锐 B.直 C.钝
(4)如图,淘气不小心将同学画的三角形弄脏了,被遮住的那两个角的度数可能是( )。
A.80°和 50°
B.100°和 10°
C.90°和 30°

(1)如果一个三角形中两个内角的和是 90°,那么这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
(2)锐角三角形 ABC 中,∠1 + ∠2 一定( )。

A.大于 90°
B.小于 90°
C.等于 90°
(3)等腰三角形一定有两个内角相等,而且这两个相等的内角一定是( )角。
A.锐 B.直 C.钝
(4)如图,淘气不小心将同学画的三角形弄脏了,被遮住的那两个角的度数可能是( )。
A.80°和 50°
B.100°和 10°
C.90°和 30°

答案:
B@@A@@A@@A
4. 求出下面各角的度数。
 ∠1 = ________
∠1 = ________
 ∠2 = ________
∠2 = ________
 ∠3 = ________
∠3 = ________
 ∠1 = ________
∠1 = ________ ∠2 = ________
∠2 = ________ ∠3 = ________
∠3 = ________
答案:
$80^{\circ}$@@$35^{\circ}$@@$48^{\circ}$
5. 求出∠1、∠2 的度数。

答案:
$\angle1 = 180^{\circ}-90^{\circ}-54^{\circ}=36^{\circ}$
$\angle2 = 180^{\circ}-90^{\circ}-36^{\circ}=54^{\circ}$
解析:先看三角形$ABC$,已知$\angle ABC = 90^{\circ}$,$\angle C = 54^{\circ}$,用$180^{\circ}$减去这两个角的度数,就是$\angle1$的度数。$180^{\circ}-90^{\circ}-54^{\circ}=36^{\circ}$。再看三角形$ABO$,已知$\angle AOB = 90^{\circ}$,用$180^{\circ}$分别减去$\angle AOB$和$\angle1$这两个角的度数,就是$\angle2$的度数,$180^{\circ}-90^{\circ}-36^{\circ}=54^{\circ}$。
6. 一个直角三角形被剪去一个直角,剩下图形的内角和是多少度?
答案:
$180^{\circ}$或$360^{\circ}$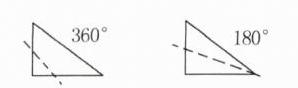
$180^{\circ}$或$360^{\circ}$
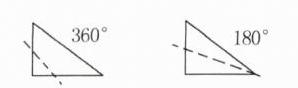
查看更多完整答案,请扫码查看


