《2025年亮点给力计算天天练六年级数学下册苏教版》

1. 直接写出得数。
$\frac{1}{35}+\frac{7}{35}=$ $25\%\times4=$ $\frac{3}{5}\div\frac{5}{3}=$ $\frac{5}{14}+\frac{7}{9}+\frac{9}{14}=$
$11\%-2\%=$ $55\%+45\%=$ $\frac{3}{10}\times\frac{5}{6}=$ $36\times(\frac{1}{2}-\frac{1}{6})=$
$0.17\times3=$ $16\div0.8=$ $63\div50\%=$ $24\div(1 - 70\%)=$
$40\%\div\frac{2}{3}=$ $\frac{4}{5}-40\%=$ $3 - 2\%=$ $1 - 5\%\times\frac{2}{5}=$
$0.88 + 30\%=$ $2.2\times0.6=$ $74\times5\%=$ $9\div0.3\times0.03=$

答案： $\frac{8}{35}$ 1 $\frac{9}{25}$ $1\frac{7}{9}$
0.09 1 $\frac{1}{4}$ 12
0.51 20 126 80
0.6 0.4 2.98 0.98
1.18 1.32 3.7 0.9

2. 计算下面各题，能简算的要简算。
$(24 - 11)\times15 - 75$ $32\times25\%\times125\%$ $9.25\times9.9 + 92.5\%$

答案： 120 10 92.5

3. 解方程。
$3x + 60\%x = 4.32$ $0.6x + 1.4\times50\% = 18.7$ $1 - 70\%x = \frac{14}{15}$

答案： $x = 1.2$ $x = 30$ $x = \frac{2}{21}$

思维提升 裂项法巧算
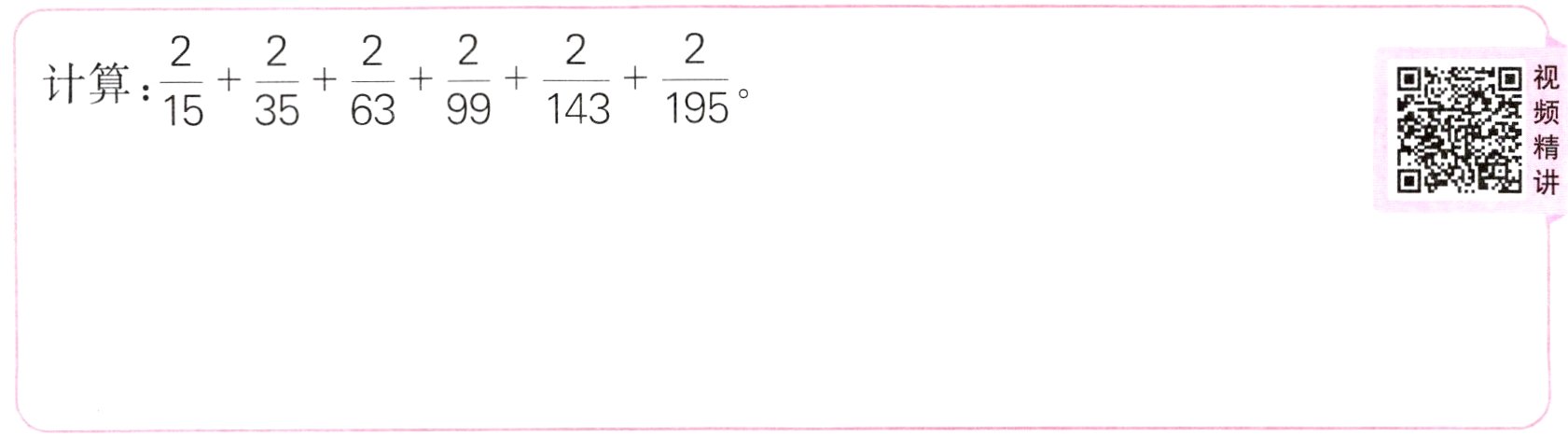
计算：$\frac{2}{15}+\frac{2}{35}+\frac{2}{63}+\frac{2}{99}+\frac{2}{143}+\frac{2}{195}$。

答案： 原式 = $\frac{2}{3 \times 5} + \frac{2}{5 \times 7} + \frac{2}{7 \times 9} + \frac{2}{9 \times 11} + \frac{2}{11 \times 13} + \frac{2}{13 \times 15}$
= $\frac{1}{3} - \frac{1}{5} + \frac{1}{5} - \frac{1}{7} + \frac{1}{7} - \frac{1}{9} + \frac{1}{9} - \frac{1}{11} + \frac{1}{11} - \frac{1}{13} + \frac{1}{13} - \frac{1}{15}$
= $\frac{1}{3} - \frac{1}{15}$
= $\frac{4}{15}$