(17)(本小题满分12分)

已知向量a＝(sinθ，1)，b＝(1，cosθ)，－＜θ＜．

(Ⅰ)若a⊥b，求θ；

(Ⅱ)求｜a+b｜的最大值．

(18)(本小题满分12分)

某批产品成箱包装，每箱5件．一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．

(Ⅰ)用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；

(Ⅱ)若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品级用户拒绝的概率．

(19)(本小题满分12分)

如图，在直三棱柱ABC－A₁B₁C₁中，AB＝BC，D、E分别为BB₁、AC₁的中点．

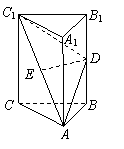(Ⅰ)证明：ED为异面直线BB₁与AC₁的公垂线；

(Ⅱ)设AA₁＝AC＝AB，求二面角A₁－AD－C₁的大小．

(20)(本小题满分12分)

设函数f(x)＝(x+1)ln(x+1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围．

(21)(本小题满分14分)

已知抛物线x²＝4y的焦点为F，A、B是抛物线上的两动点，且＝λ(λ＞0)．过A、B两点分别作抛物线的切线，设其交点为M．

(Ⅰ)证明·为定值；

(Ⅱ)设△ABM的面积为S，写出S＝f(λ)的表达式，并求S的最小值．

(22)(本小题满分12分)

设数列{a_n}的前n项和为S_n，且方程x²－a_nx－a_n＝0有一根为S_n－1，n＝1，2，3，…．

(Ⅰ)求a₁，a₂；

(Ⅱ){a_n}的通项公式．

普通高等学校招生全国统一考试