(17)(本小题满分12分)
在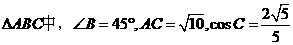 ,求
,求
(1)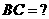
(2)若点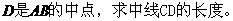
(18)(本小题满分12分)
设等比数列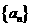 的前n项和为
的前n项和为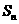 ,
,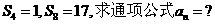
(19)(本小题满分12分)
某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品。
(I)求取6件产品中有1件产品是二等品的概率。
(II)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率。
 (20)(本小题12分)
(20)(本小题12分)
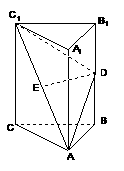
如图,在直三棱柱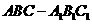 中,
中,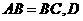 、
、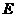 分别为
分别为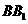 、
、 的中点。
的中点。
(I)证明:ED为异面直线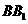 与
与 的公垂线;
的公垂线;
(II)设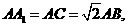 求二面角
求二面角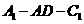 的大小
的大小
(21)(本小题满分为14分)
设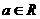 ,函数
,函数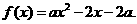 若
若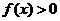 的解集为A,
的解集为A,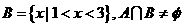 ,求实数
,求实数 的取值范围。
的取值范围。
(22)(本小题满分12分)
已知抛物线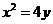 的焦点为F,A、B是抛物线上的两动点,且
的焦点为F,A、B是抛物线上的两动点,且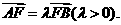 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明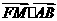 为定值;
为定值;
(II)设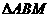 的面积为S,写出
的面积为S,写出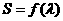 的表达式,并求S的最小值。
的表达式,并求S的最小值。
普通高等学校招生全国统一考试(全国II卷)
- 答案

