14.已知n次式项式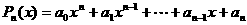 .
.
如果在一种算法中,计算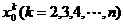 的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要
的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要
次运算.
下面给出一种减少运算次数的算法:P0(x)=a0,Pk+1(x)=xPk(x)+ak+1(k=0,1,2,…,n-1).利用该算法,计算P3(x0)的值共需要6次运算,计算P10(x0)的值共需要
次运算.
[答案]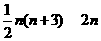
[详解]
由题意知道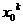 的值需要
的值需要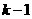 次运算,即进行
次运算,即进行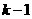 次
次 的乘法运算可得到
的乘法运算可得到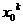 的结果
的结果
对于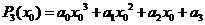 这里
这里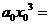
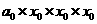 进行了3次运算,
进行了3次运算,
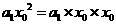 进行了2次运算,
进行了2次运算,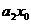 进行1次运算,最后
进行1次运算,最后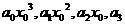 之间的加法
之间的加法
运算进行了3次这样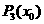 总共进行了
总共进行了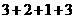
 次运算
次运算
对于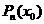
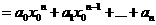 总共进行了
总共进行了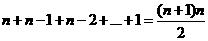 次
次
乘法运算及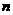 次加法运算所总共进行了
次加法运算所总共进行了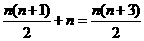 次
次
由改进算法可知:
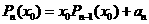 ,
,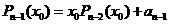
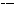
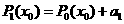 ,
,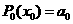
运算次数从后往前算和为: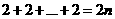 次
次
[名师指津]
本题目属于信息题,做此类题需要认真分析题目本身所给的信息.
- 答案

