15.(本小题共13分)
已知函数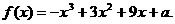
(Ⅰ)求 的单调减区间;
的单调减区间;
(Ⅱ)若 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
[答案]
[详解]
解:(I)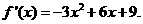
令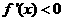 ,解得
,解得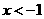 或
或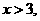
所以函数 的单调递减区间为
的单调递减区间为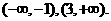
(II)因为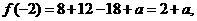
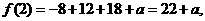
所以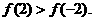
因为在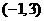 上
上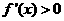 ,所以
,所以 在
在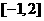 单调递增,又由于
单调递增,又由于
 在
在 上单调递减,因此
上单调递减,因此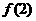 和
和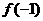 分别是
分别是 在区间
在区间
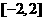 上的最大值和最小值.
上的最大值和最小值.
于是有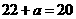 ,解得
,解得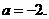
故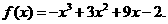
因此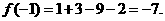
即函数 在区间
在区间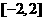 上的最小值为
上的最小值为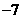

[名师指津]
函数求导的方法研究函数的单调性及最值问题近几年高考试题中屡屡出现,成为热门题型.要
熟练掌握各种常见函数的求导方法及研究单调、最值的基本思路.
- 答案

