16.(本小题共14分)
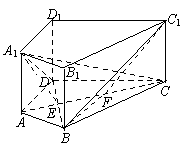
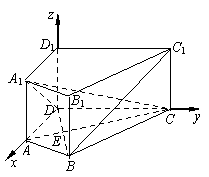
 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=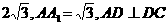 ,
,
AC⊥BD,垂足为E.
(Ⅰ)求证BD⊥A1C;
(Ⅱ)求二面角A1-BD-C1的大小;
(Ⅲ)求异面直线AD与BC1所成角的余弦值.
 解法一:
解法一:
(I)在直四棱柱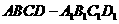 中,
中,
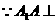 底面
底面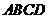 ,
,
 是
是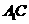 在平面
在平面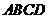 上的射影.
上的射影.
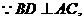
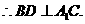
(II)连结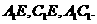
与(I)同理可证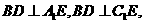
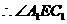 为二面角
为二面角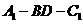 的平面角.
的平面角.
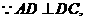
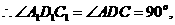
又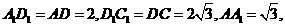 且
且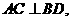
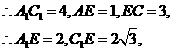
在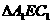 中,
中,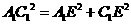 ,
, 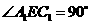 ,
,
即二面角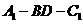 的大小为90°
的大小为90°
(III)过B作BF∥AD交 于
于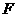 ,连结
,连结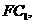
则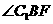 就是
就是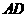 与
与 所成的角.
所成的角.
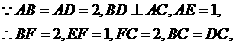

在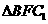 中,
中,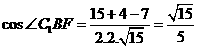 。
。
即异面直线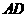 与
与 所成角的余弦值为
所成角的余弦值为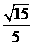 。
。
 解法二:
解法二:
(I)同解法一.
(II)如图,以D为坐标原点,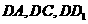 所
所
在直线分别为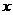 轴,
轴,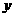 轴,
轴,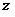 轴,建立空间
轴,建立空间
直角坐标系.
连结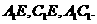
与(I)同理可证,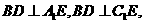
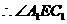 为二面角
为二面角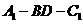 的平面角.
的平面角.
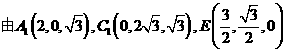
得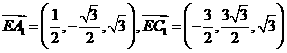 。
。
∴ 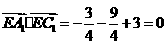 。∴
。∴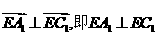 。
。
∴ 二面角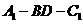 的大小为90°.
的大小为90°.
(II)如图,由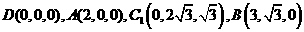 ,得
,得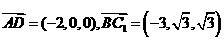 。
。
∵ 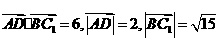 ,
,
∴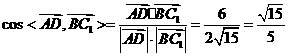 。
。
即异面直线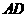 与
与 所成角的余弦值为
所成角的余弦值为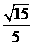 。
。
解法三:
(I)同解法一.
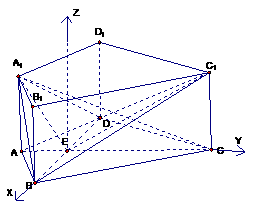 (II)如图,建立空间直角坐标,坐标原点为E.
(II)如图,建立空间直角坐标,坐标原点为E.
连结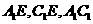
与(I)同理可证,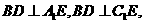
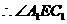 为二面角
为二面角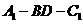 的平面角.
的平面角.
由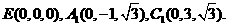
得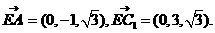
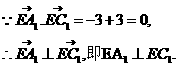
 二面角
二面角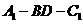 的大小为
的大小为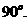
(III)如图,由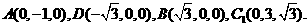
得
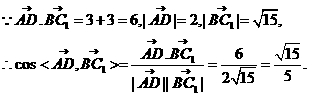
 异面直线
异面直线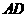 与
与 所成角的大小为
所成角的大小为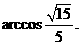
[名师指津]
三垂线定理,二面角的平面角、线面角、两条异面直线所成的角作法及求法,线线、线面、面面平
行与直线的判断与性质,构成了立体几何的主要内容,平时学习时应将之落实.
- 答案

